The Honours Project was completed at the Chair for Computation in Engineering and was supervised by Dipl.-Ing. Tino Bog.
Introduction
The interaction between different parts in a mechanical system plays a pivotal role in several fields of engineering. The correct representation of these interaction falls into the realm of contact mechanics. Numerical approximations of contact problems are predominantly obtained by means of the Finite Element Method (FEM). In the science community, historically effort has been mostly put in the standard h-version of the FEM, which employs a linear ansatz order for the discretization of the geometry and the solution field. This is obviously a drawback when complex, curved geometries have to be simulated, namely in the description of the contact surface and in terms of meshing effort. Therefore in the scope of this project, a fictitious domain method which makes use of high order shape functions known as the Finite Cell Method (FCM) [1] is utilized to avoid these problems. Regarding the enforcement of contact constraints, the prevailing approaches are the penalty method and the Lagrange multipliers method. In this project however, a more exotic technique has been used, which related to a third medium approach proposed by Wriggers in [2] and will be referred to as Fictitious Material Approach in the following.
The Finite Cell Method
A way to mitigate the difficulties related to meshing complex geometries exploits the usage of fictitious domain methods, which do not required a conforming discretization of the problem. One such method is the Finite Cell Method. The main idea is to embed the physical domain into a simpler domain, usually with a Cartesian shape. The geometry of the physical bodies is then recovered at integration level by using a step function α(X), which takes the value one if the point lies in the physical part of the domain and zero (numerically small) otherwise. As a consequence the bilinear form is modified as follows:
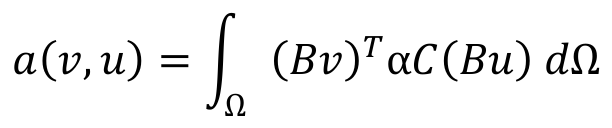
Equation 1): Modified bilinear form for the Finite Cell Method.
where the linear operator can be rewritten analogously. A simple and fast way to implement the inside/outside test needed for assigning a value to α is by using a spacetree partitioner. For a more thorough description and other possibilities the reader is referred to [3].
Fictitious Material Approach
The procedure of filling gaps and voids within the Fictitious Material Approach [4] resembles closely the FCM concept. However, in this case the contact material is ought to stiffen as contact surfaces come close to one another. This change in the contact material stiffness is the key for the enforcement of the contact constraint and therefore a thorough investigation of different material formulations has been carried out as starting point of this work. It is worth noting that this approach can be categorized as a barrier method since it does not allow for interpenetration between bodies coming into contact. In figure 1) a comparison of several hyper-elastic formulations and the anisotropic model proposed by Wriggers in [2] is shown, where on the x-axis the principal stretch in the direction of contact is plotted against the corresponding principal stress. The latter quantities can be related with the gap between the bodies coming into contact and the contact reaction force respectively. This can be formally formulated as the well-known Kuhn-Tucker condition:
g ≥ 0, R ≤ 0, g · R = 0
where g is the gap and R the normal reaction force.
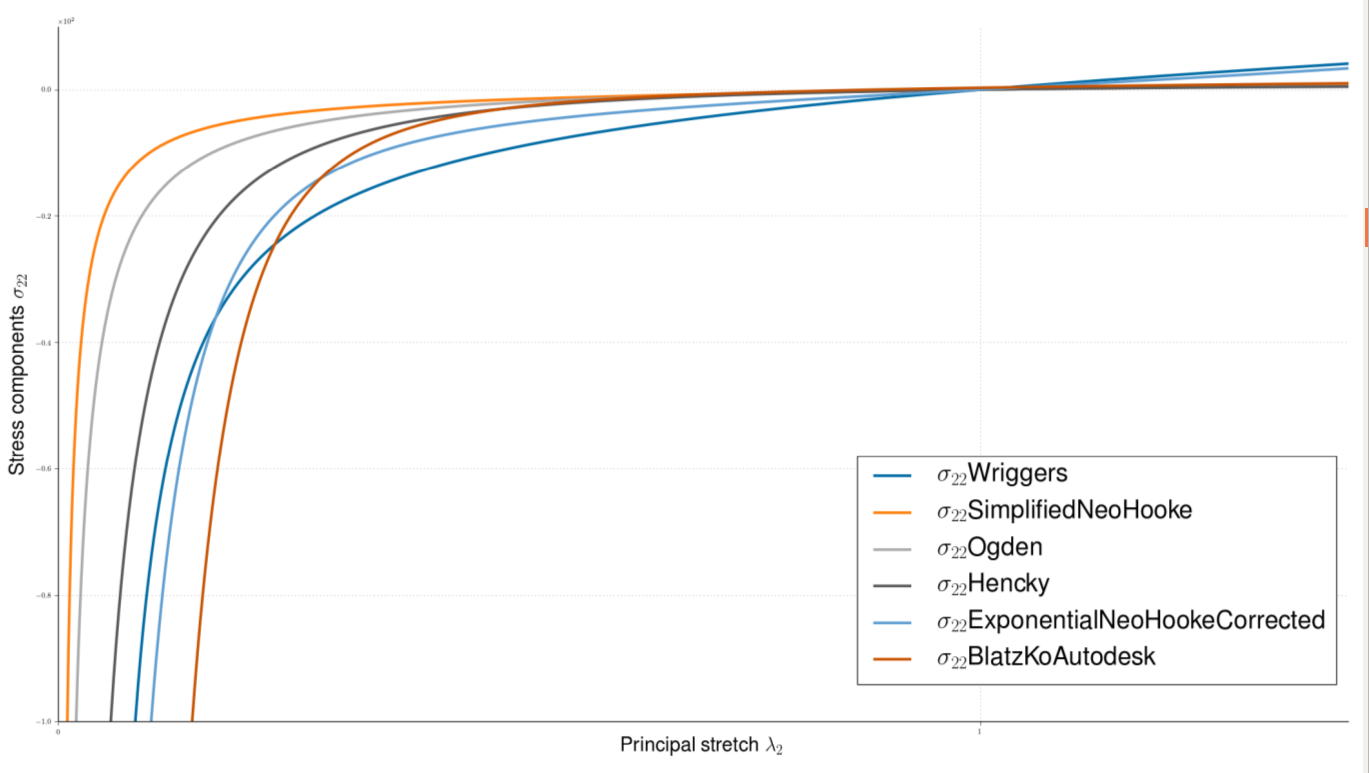
Figure 1): Comparison of different material formulations for the fictitious contact material approach.
It can be stated that qualitatively all the formulations behave in a similar manner in approximating the Kuhn-Tucker condition. Therefore in all the numerical examples presented in the following, the Simplified Neo-Hooke model has been utilized, since its description requires only one parameter. The strain energy potential is written as follows:
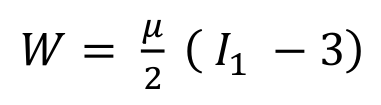
Equation 2): Strain energy function for the simplified Neo-Hookean formulation.
where μ is the first Lamè parameter and I1 is the trace of the right Cauchy-Green deformation tensor. For a detailed review of continuum mechanics the reader is referred to [5].
Numerical results
The first numerical benchmark that has been investigated is the well-known frictionless Hertzian contact problem of a cylinder impacting a rigid plane. Exploiting symmetries only one quarter of the circular section of the cylinder is modelled, as shown in figure 2). In figure 2) is also displayed the stress distribution in the vertical direction for a mesh formed by 3×2 p-element.
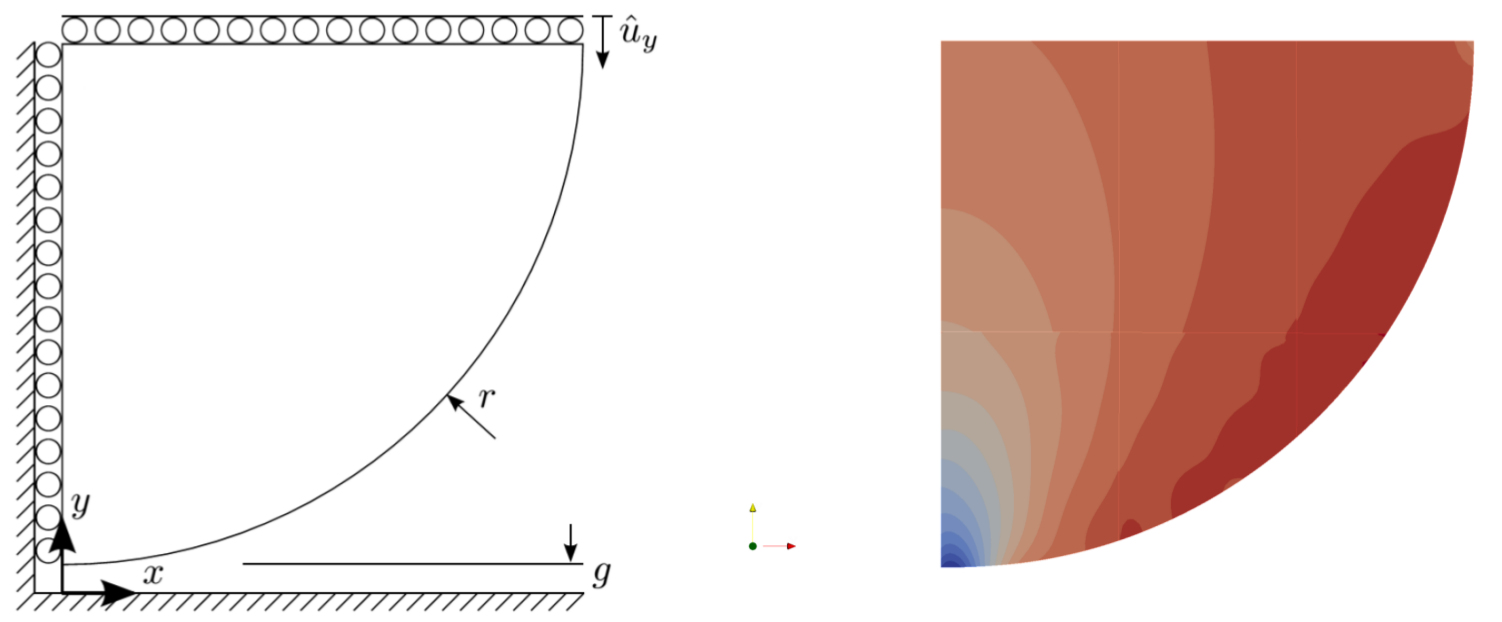
Figure 2): Problem description on the left and stress distribution in the vertical direction on the right (p = 5).
For the problem at hand, the normal pressure distribution along the circular boundary can be computed analytically in a closed form, this corresponds to the black curve in figure 3). The other curves represent the numerical pressure for different increasing ansatz orders, where an adaptive hierarchical refinement scheme has been employed to better capture the kink in the analytical solution. It can be stated that increasing the polynomial order of the shape functions leads to a reduction of the error in the 2-norm.
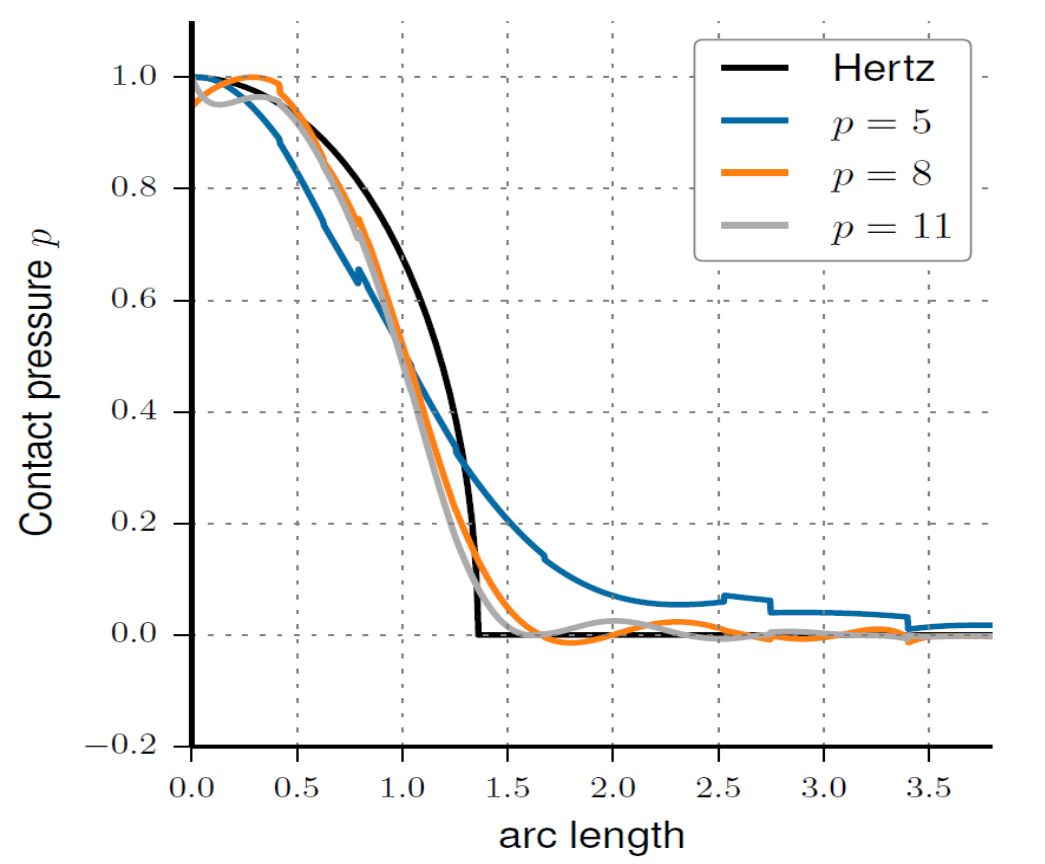
Figure 3): Comparision of the numerical contact pressure against the analytical solution performing p-refinement.
The next example tackles the issue derived from self-contact problems. It should be stated at this point that self-contact and extension to 3-D applications do not require additional effort, in contrast to the majority of conventional methods. In figure 4) the displacement distribution is visualized and compared to a standard finite element analysis obtained with the commercial software ANSYS®.
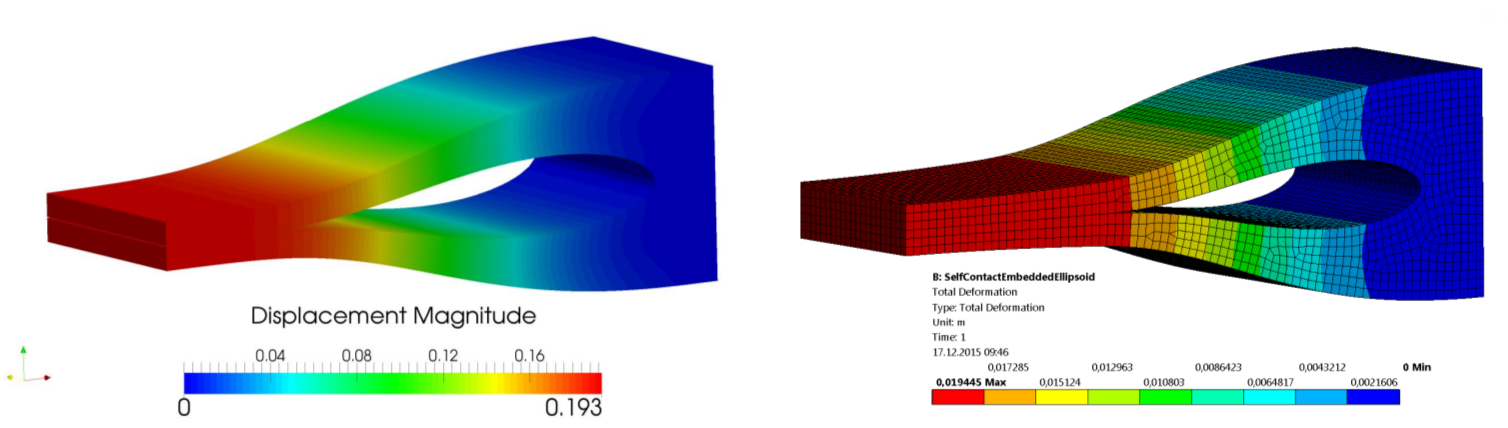
Figure 4): Displacement distribution of the self-contact 3D example against the same setup computed with ANSYS®.
References
[1] J. Parvizian, A. Düster, E. Rank, Finite cell method, Computational Mechanics 41 (1), 2007.
[2] P. Wriggers, J. Schröder, A. Schwarz, A finite element method for contact using a third medium, Computational Mechanics 52 (4), 2013.
[3] L. Kudela, N. Zander, T. Bog, S. Kollmannsberger, E. Rank, Efficient and accurate numerical quadrature for immersed boundary methods Advanced Modeling and Simulation in Engineering Sciences 2 (1), 2015.
[4] T. Bog, N. Zander, S. Kollmannsberger, E. Rank, Normal contact with high order finite elements and a fictitious contact material, Computers & Mathematics with Applications 70 (7), 2015.
[5] J. Bonet, R. D. Wood, Nonlinear Continuum Mechanics For Finite Element Analysis, 2nd Edition, Cambrigde University Press, Cambrigde, 2008.
