Navaneeth K Narayanan did his honour’s project at the Chair of Structural Analysis (TUM) and
was supervised by Aditya Ghantasala M.Sc and PD Dr.-Ing. habil. Roland Wüchner.
Computational fluid dynamics simulation involving large relative motion of solid bodies is quite challenging. One way to perform such simulations is to remesh the domain at every time step according to the updated positions of solid bodies,which is quite expensive. There are some alternatives such as embedded approach, mesh-free method etc. which allows arbitrary movement of solid bodies. But among the various methods that are available, chimera method offers best combination of lower computational cost and accuracy with the least modification in the existing framework. Each component in the domain are meshed independently, and are coupled at the overlapping boundaries in the solution process, to get a global solution field. Since each mesh around components are independent, they are free to move with respect to each other. This way chimera method offers great flexiblity in movement of the solid bodies in the fluid domain. The present project work is an attempt to implement monolithic chimera method in finite element framework for fluids with variational multiscale formulation. This coupling was achieved by formulating the coupling conditions as a multi-point constraint.
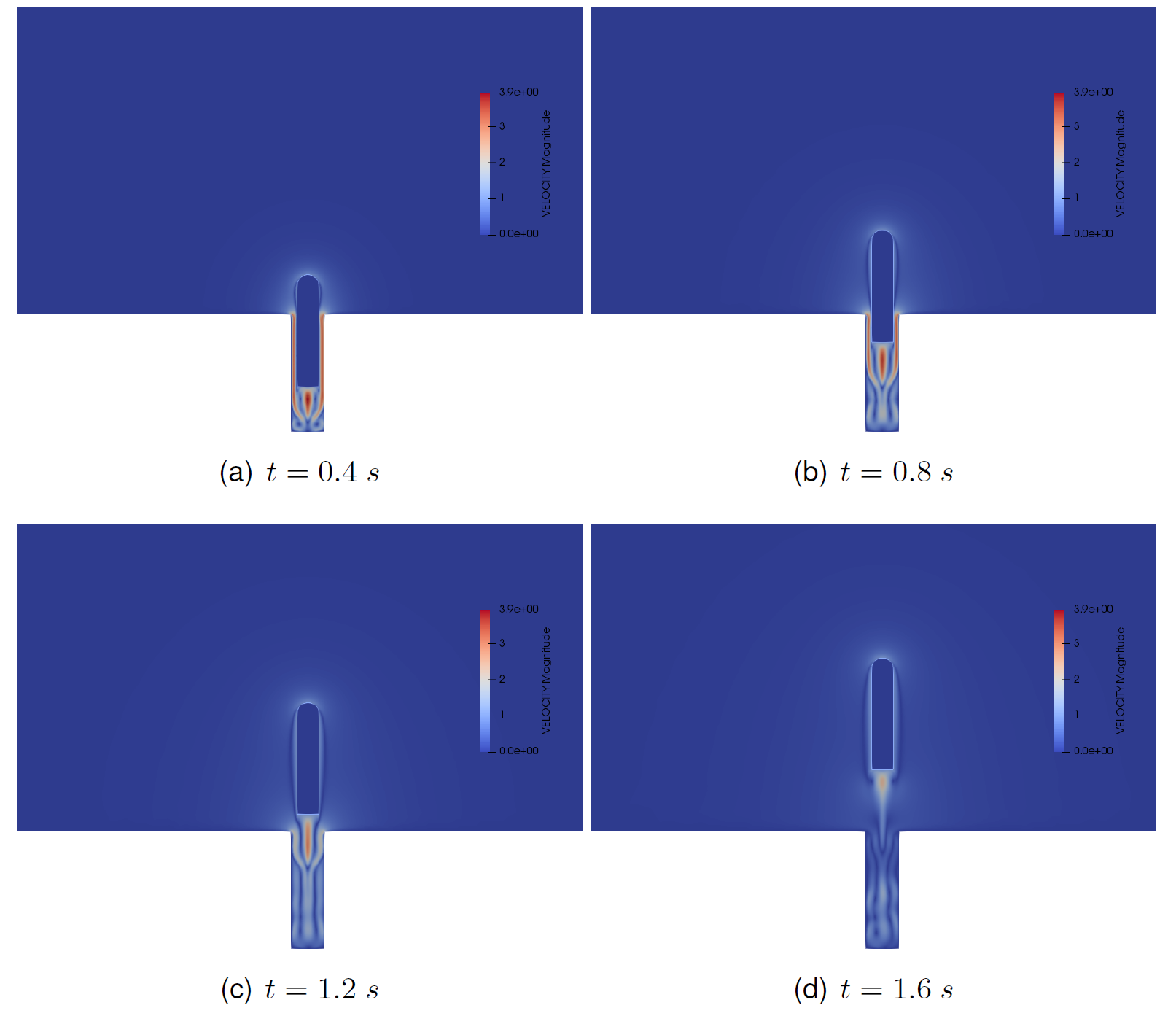
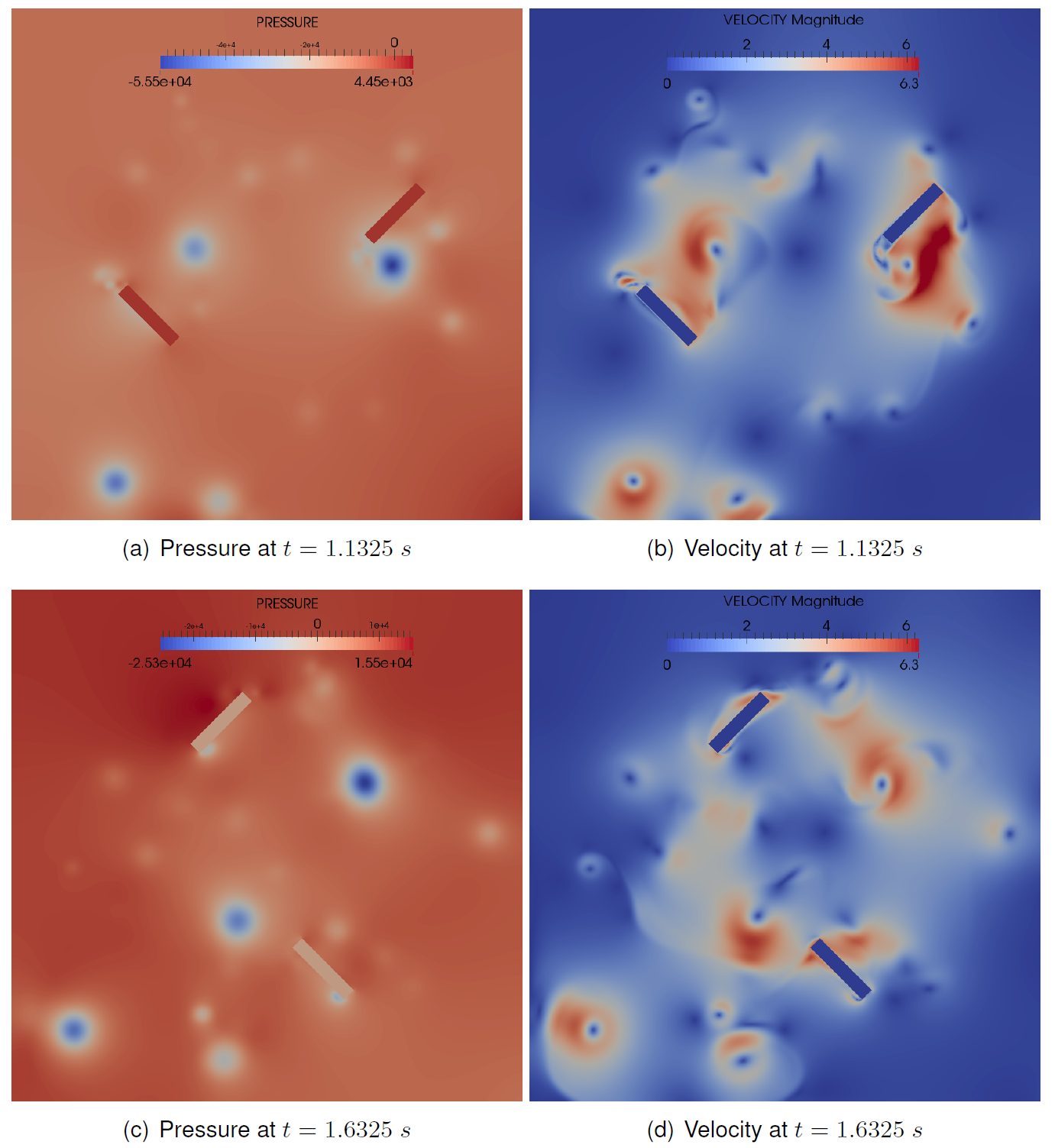
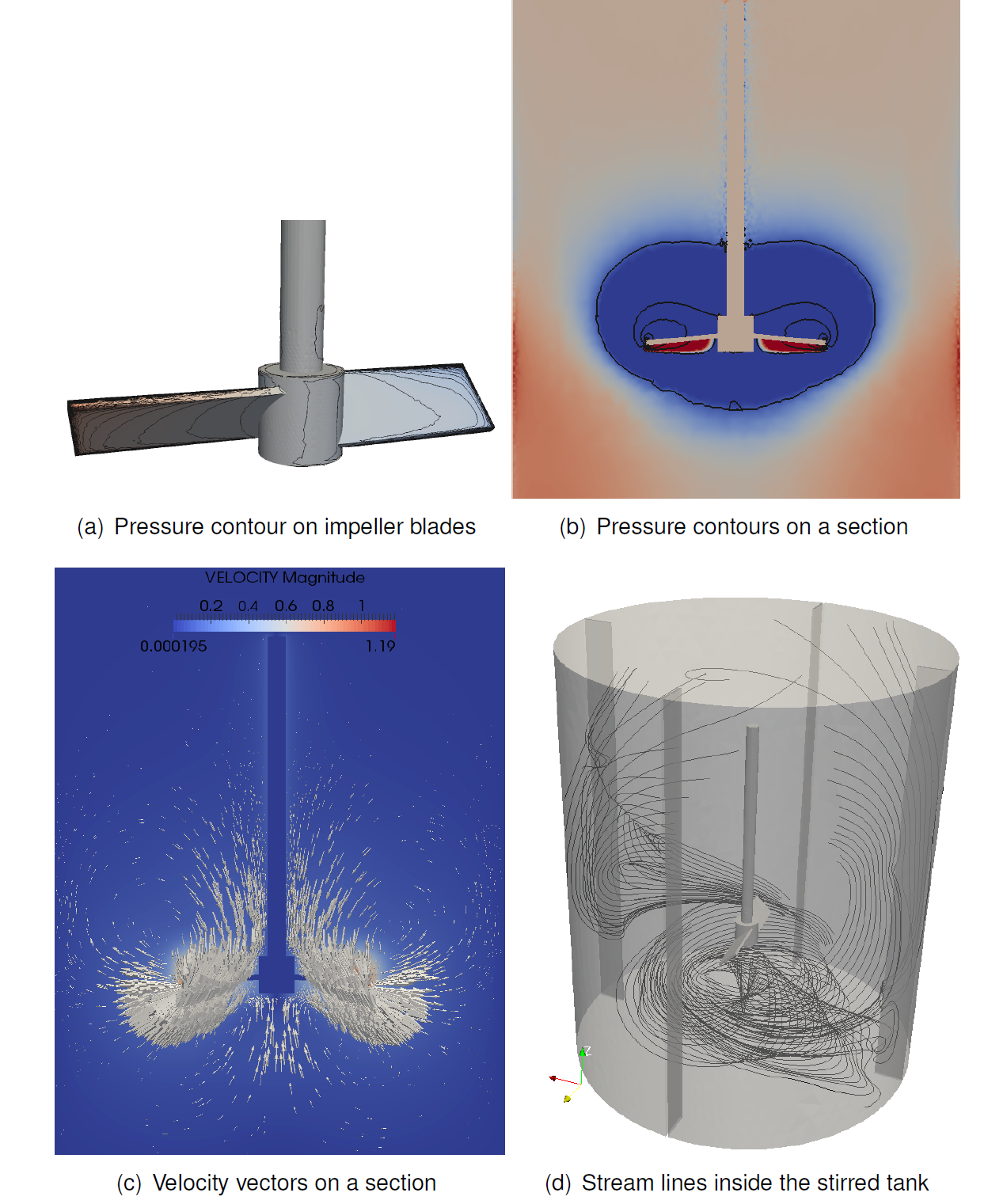
The implemented framework can simulate flow around multiple bodies in a background which are in relative motion with respect to each other. However, it cannot handle cases where bodies are very close to each other, when patches intersect. Several simulation cases were considered with increasing level of complexity to demostrate the potential in this method to perform moving body fluid flow simulations, which is otherwise not possible in conventional CFD technique. Figure 1 shows the velocity field around a missile launched from a submarine. Here, the computational domain consist of a rectangular patch around the missile which moves along with it in a stationary background mesh (not shown in the figure). The next simulation case is more complex than the first one, where there are two patches around the blades moving with respect to each other. The problem under consideration is the flow in a closed box driven by two moving plates, which resembles a mixer, shown in figure 2. Finally, figure 3 shows an application of chimera method in a 3D case. For this, we consider a cylindrical tank which consist of an axial flow impeller with four baffles welded at the cylider wall. The impeller has two 45 degrees pitched blades which draws the fluid from the top and pushes at the bottom of the tank. Here the two blades and the shaft are enclosed in cylindrical patch embedded in a background mesh covering the entire tank.
 |
 |
 |
