Daniela Anderl, Nan Chen, Matthias Grießinger, and Moritz Kreutzer did their honours project under the supervision of Björn Gmeiner (LSS, FAU).
Within this project, two mesh-based PDE solvers, namely Hierarchical Hybrid Grids (HHG) and the Peano framework should be compared. Both of them use multigrid to solve PDEs. Furthermore, both are designed to have a low memory consumption, hardware efficient execution and a high degree of parallelism. Due to problems with Peano, tests were only performed with HHG.
HHG
HHG is developed at the Department of System Simulation at the Friedrich-Alexander- University Erlangen-Nuremberg. It is designed to close the gap between the flexibility of finite elements and the high performance of geometric multigrid.
Due to the lack of an explicit storage of the stiffness matrix, the limitations on the problem size known from ordinary finite element solvers are removed. Furthermore, the memory requirements are reduced drastically. For the intern representation of the geometry a compromise between structured and unstructured grids is made. Hierarichal Hybrid Grids are basically a variant of blockstructured (i.e. semi- structed) grids. The coarse input mesh, which should resolve the geometry and the material parameters of the geometry, is organized into grid primitives, namely vertices, edges, faces and volumes. These primitives are refined in a structured way, thus creating a nested hierarchy of grids. On these structured patches stencils are used for computation.
The data structures of HHG are implemented in form of a C++ library, whereas the numerical kernels are implemented in Fortran 77. There are several choices for the coarse grid solver, e.g., an algebraic multigrid solver (BoomerAMG), LU decomposition (SuperLU), the Conjugate Gradient Method, etc. The Finite element discretization is done with linear basis functions. Furthermore, HHG comprises a MPI communication model. In fact, it is a one-way communication model for updating the local dependencies.
Task
For performance analysis, several computer architectures were used, including distributed-memory multi core architectures to investigate the parallel efficiency. The comparison criteria are
- the convergence behavior
- the memory requirements,
- the performance behavior and
- the parallel efficiency.
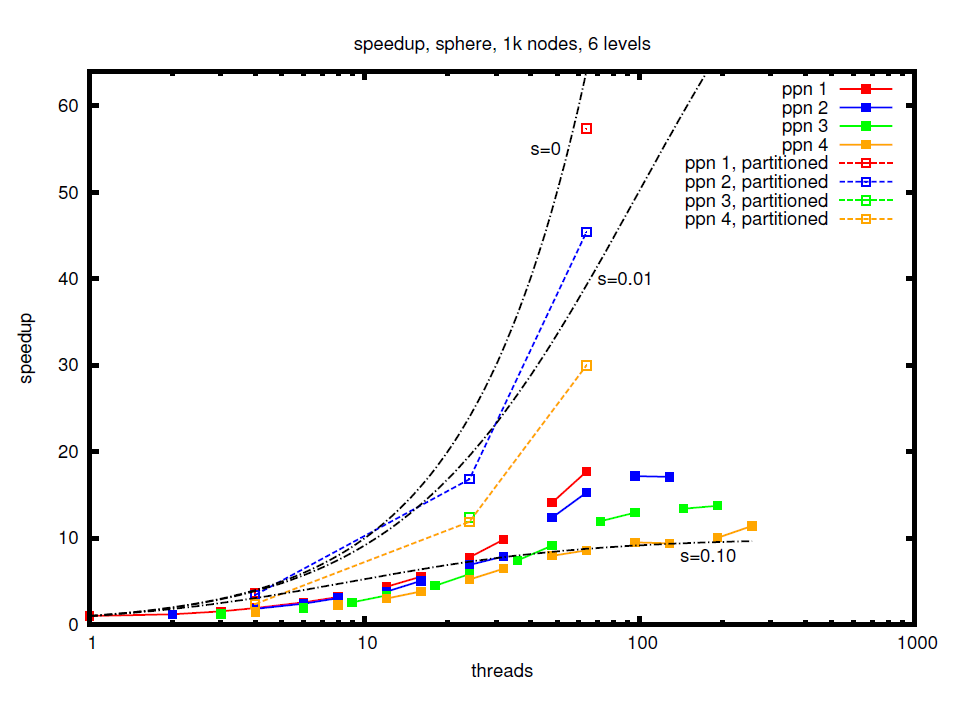
Therefore, two tests on cube-, sphere- and L-shaped domains were performed on the Woody and Tinyblue clusters of the Erlangen Regional Computing Centre. An example for the speedup achieved in a strong sclaing experiment on the unit sphere is shown in the figure.
Report
The detailed project report can be found here.
