under supervision by
Dr. Dirk Hartmann (Siemens Coporate Technology / Simulation Digital Twin)
Andres Botero Halblaub (Siemens Coporate Technology / Simulation Digital Twin)
M.Sc. with honors Friedrich Menhorn (TUM)
Motivation
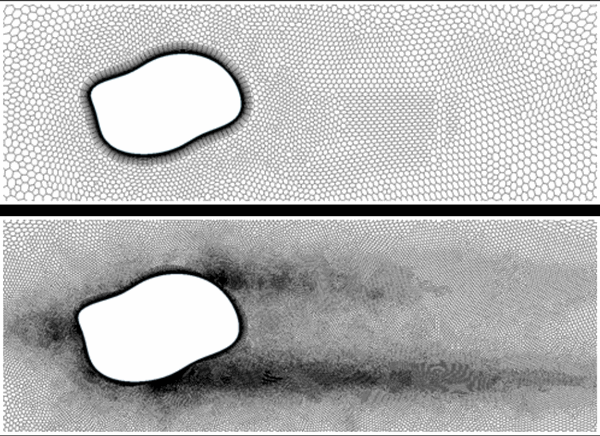
Mesh creation and refinement is one of the most time-consuming steps in any CFD simulation; even automated mesh generation requires high levels of expertise and fine-tuning. This project attempts to circumvent some of this complexity by leveraging deep convolutional neural networks to predict mesh densities for arbitrary geometries. Such a refined mesh can be seen in Fig. 1.
An automated pipeline was created to generate random geometries and run CFD simulations, iteratively performing targetted mesh refinement utilizing adjoint sensitivies. A comprehensive 6TB dataset consisting of 65,000 geometry-mesh pairs was assembled via an extensive post-processing and evaluation setup.
Current literature indicated that the UNet architecture extended by Thuerey et al. was suitable to predict flow-related quantities, but had never been used for mesh prediction. In this work, we present a deep, fully convolutional network that estimates mesh densities based off geometry data. The most recent model, tuned with hyper-parameters like network depth, channel size and kernel size, had an accuracy of 98% on our validation dataset.
The current pipeline provides a proof-of-concept that convolutional neural networks can, for specific use-cases, generate accurate mesh densities without the need manual fine-tuning. Such a product, if further tuned and extended, can provide significant time savings in future CFD workflows, completely independent of personnel expertise.
Setup
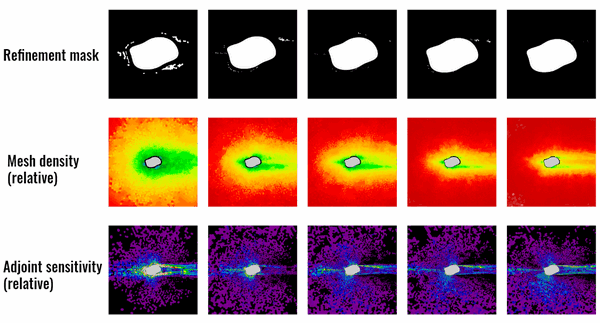
As with all machine learning, training a successful network requires a lot of training data. For our particular case, there was no large dataset of refined meshes for random geometries available, so we had to create it ourselves. This is not a trivial task. As mentioned above, creating refined meshes for complex geometries for cfd simulation is usually an experts task. In our case, it would have been too time consuming to create tens of thousands of meshes manually.
Therefore, we used the adjoint solver built in to Star-CCM+ to investigate the sensitivity of the drag force with respect to refinement of individual mesh cells. If a cell shows a high sensitivity (as seen in Fig. 2 bottom), it is very likely that “cutting the cell” into smaller subcells would reduce the residual with regard to the drag force. Our iterative refinement strategy therefore used these results to determine which cells to refine and re-run the simulation with the new mesh densities. This would be repeated until a certain threshold either in residual or in refinement steps would be reached.
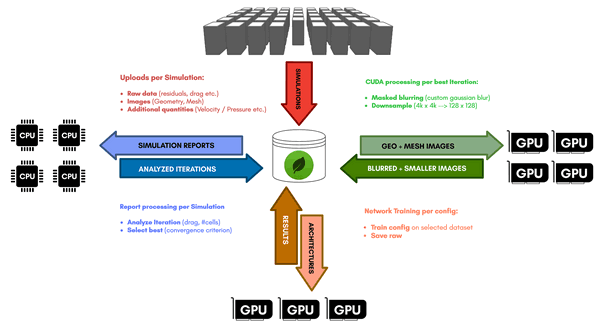
Using the CoolMUC2/3 and IvyMUC clusters at LRZ, we automated the simulation pipeline and thus simulated and optimized about 65.000 geometries and 325.000 meshes respectively. To handle the massive amounts of data we deployed a MongoDB database. We handled post-processing of both the logs coming from the simulations as well as the corresponding mesh pictures in parallel with up to 4 of our personal machines participating with their CPU and GPU power.
At the end of post-processing. We had selected a set of around 10.000 geometry-mesh pairs that had gone through the refinement iterations most successfully. The images had been down-sampled and smoothed via custom kernels implemented in CUDA to preserve sharp geometry edges. A lot of effort was put into performance-optimizing every step of the pipeline shown in Fig. 3. Even with all of this work done, a full pass through of all simulation data through post-processing still takes multiple days with the help of all of our personal machines.
During machine learning, a similar distributed approach was used. Different networks and training strategies were dispatched to multiple GPU-equipped machines and would report the final training results back to the database. During this phase, the networks were only trained for a couple of hours each to be able to test as many configurations as possible. In total, more than 200 unique network/training conditions were tested.
Results
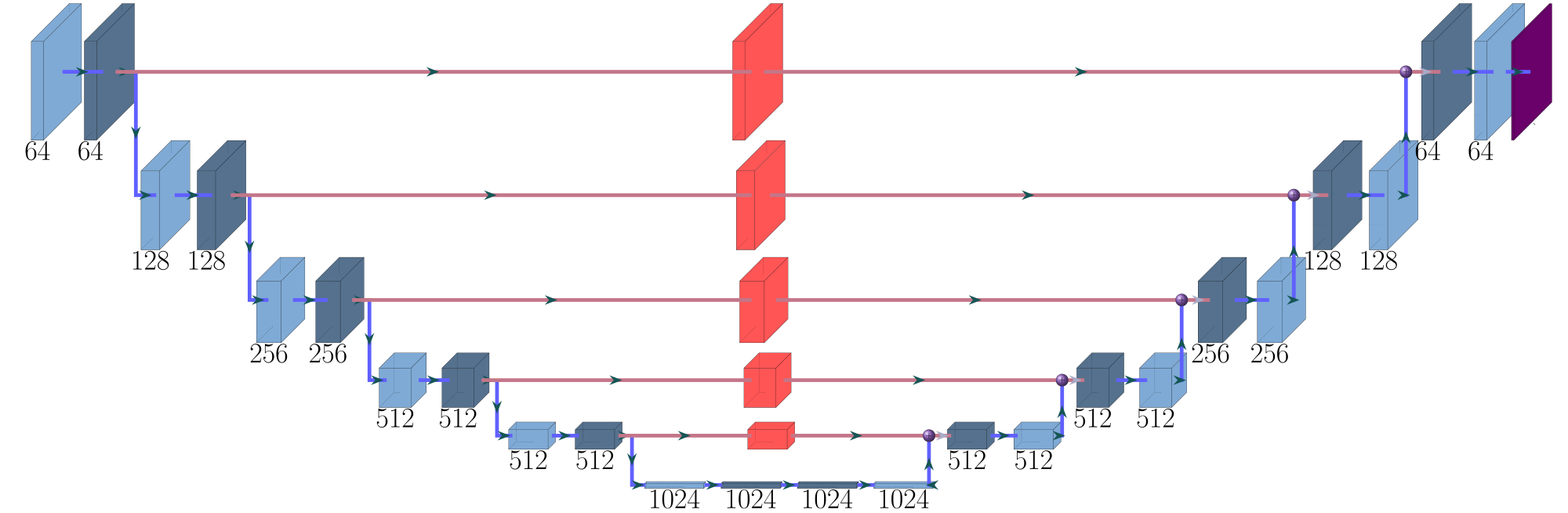
We specifically tested fully-convolutional networks with 3 different architectures. A simple down- and up-sample network, the same network with skip connections and finally a staircase architecture (Fig.4). After initial testing, promising configurations were tested on the full training set and for up to 24 hours with different training hyper-parameters like learning rate and beta-decay for the Adam Optimizer.
Finally, the best performing configuration was a staircase UNet architecture 8 layers deep and 2 layers wide on each depth with tensor skip connections at levels 2,3,4,5 and maximal kernel sizes of 16×16. During learning we used beta values beta1=0.9 and beta2=0.999. In total, this network has 8.5 x 10⁷ degrees of freedom, which means a capacity of less than 10% of the training set. The network showed no signs of overfitting and reached a final accuracy of 98.7% on the validation set.
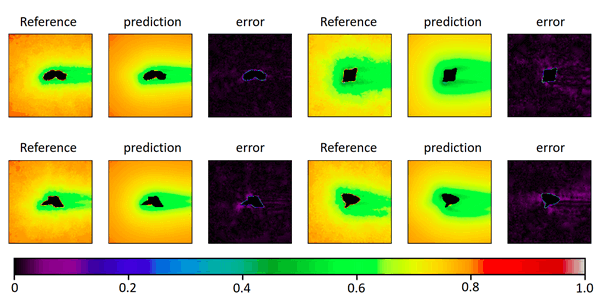
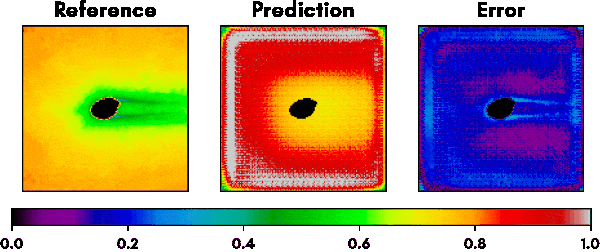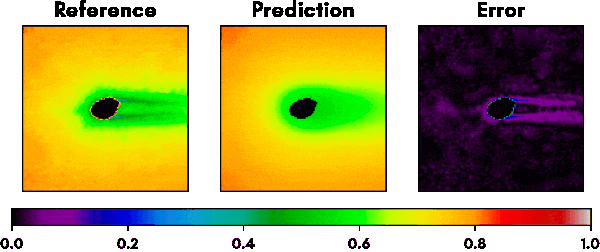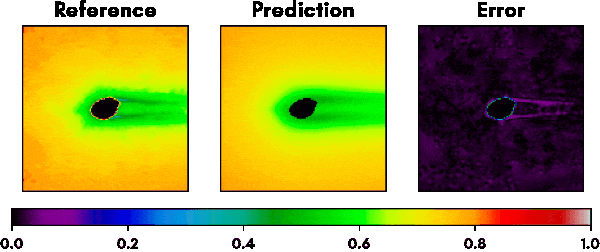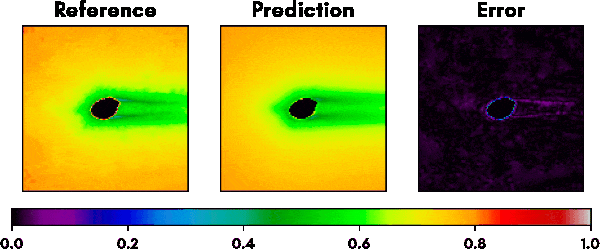
Fig. 5 shows a selection of other geometries that were part of the validation set and the performance of our trained network. The predictions regarding optimal mesh densities show a good alignment with the results from the iterative refinement algorithm.
A single forward pass through the network for a given geometry takes less than 100ms compared to about 1 hour for the iterative approach and yields reasonably similar mesh densities for even complex shapes. The network therefore could be used as a good first approximation step for getting optimized meshes and therefore save users a lot of fine tuning work when dealing with mesh creation.
We would like to thank LRZ for the compute time, NVIDIA for granting us a TitanXp GPU for this project and finally our customers at Siemens and CD-Adapco for providing us with the exciting project and continued support.
