Supervision: Dr. Roland Wüchner, Michael Breitenberger M.Sc.M.Sc.(hons) (Chair for Structural Analysis, Technische Universität München)
Motivation
Based on the paper “Isogeometric Reissner–Mindlin shell analysis with exactly calculated director vectors” a shell element for finite element analysis was implemented in the in-house code of the chair of structural analysis. The isogeometric concept allows, beside an exact geometry representation to skip the meshing process, which is usually costly in FEA. The Reissner- Mindlin theory in turn provides a shell, which is able to catch the deformation in thick cross sections.
Reissner – Mindlin shell
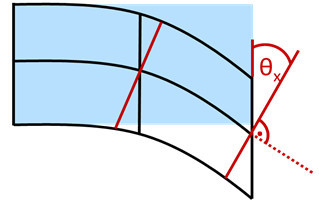
The deformation of a thick shell causes a rotation of the cross section around the mid surface (Fig.1).
 |
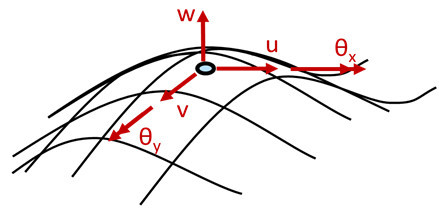 |
| Figure 1: Rotation of the director. | Figure 2: Degrees of freedom. |
This rotation occurs only in thick cross sections, for which this shell was developed. To catch this rotation additional rotational degrees of freedom are applied.
Isogeometric Concept
The isogeometric concept is related to the isoparametric concept, where the same set of shape functions is chosen for the interpolation of the displacement field and the geometry representation. The isogeometric concept works the same way, but starts with the geometry description, which is usually done with CAD and uses NURBS as basis functions.
Director Interpolation
Essential for the Reissner-Mindlin shell is the knowledge of the director. As the directors can only be computed on the surface (at the Gauss points; GP) of the shell, an inverse mapping must be performed to obtain the directors on the control points (CP):
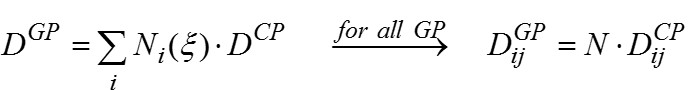
Results
As one Benchmark example the displacement for different polynomial degrees with the Scordlis Lo Roof setup was chosen.
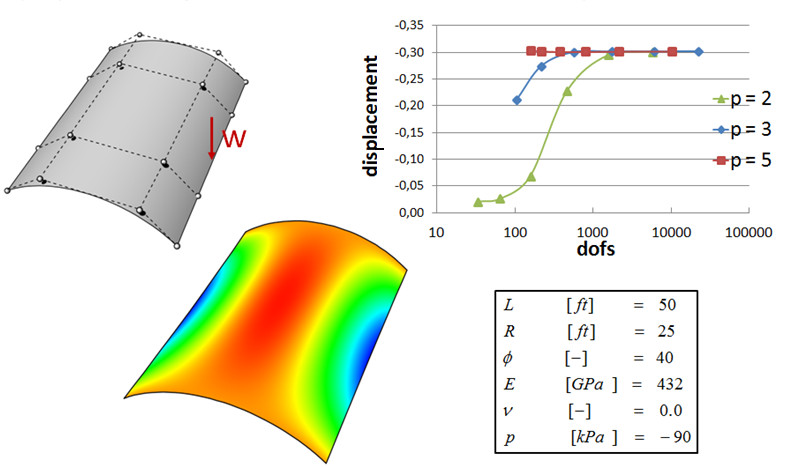
Figure 3: Scordelis-Lo Roof results.
Although the shell is slower than other similar shell formulations, it has several advantages. It is well suited for thick shells and has the possibility to represent geometry exactly. Furthermore it is possible to couple to different patches due to its additional dofs.
Reference
W. Dornisch, S. Klinkela, B. Simeon: “Isogeometric Reissner-Mindlin shell analysis with exactly calculated director vectors”, 5. September 2012, Computer Methods in Applied Mechanics and Engineering , Elsevier
