Hayden Liu Weng
Efficient and accurate methods for numerical integration are an essential element in many computational algorithms. This is especially important for the solution of partial differential equations on domains with internal interfaces where discontinuous integrands may have to be considered, such as in the Finite Cell Method, an immersed boundary method relying on high-order finite elements. One technique which successfully deals with the integration requirements is the smart octree introduced by Kudela in [1]. This space decomposition method creates boundary-conforming integration sub-cells for a composed numerical quadrature. The technique, however, is limited to boundary representation (B-Rep) geometries such as the one that is available from a CAD model.
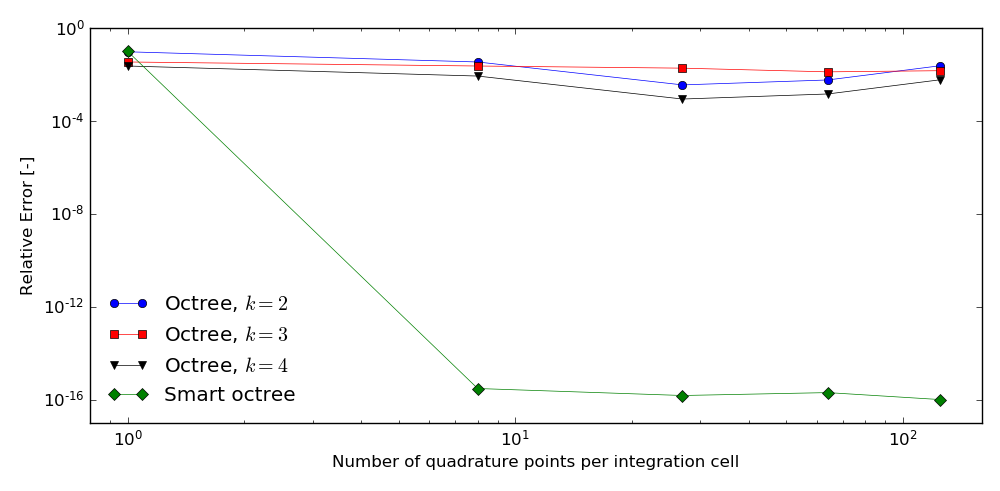
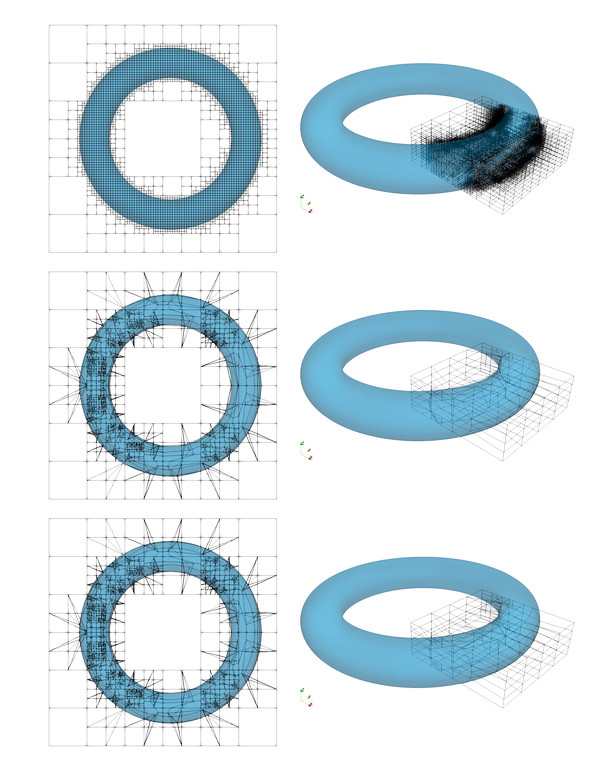
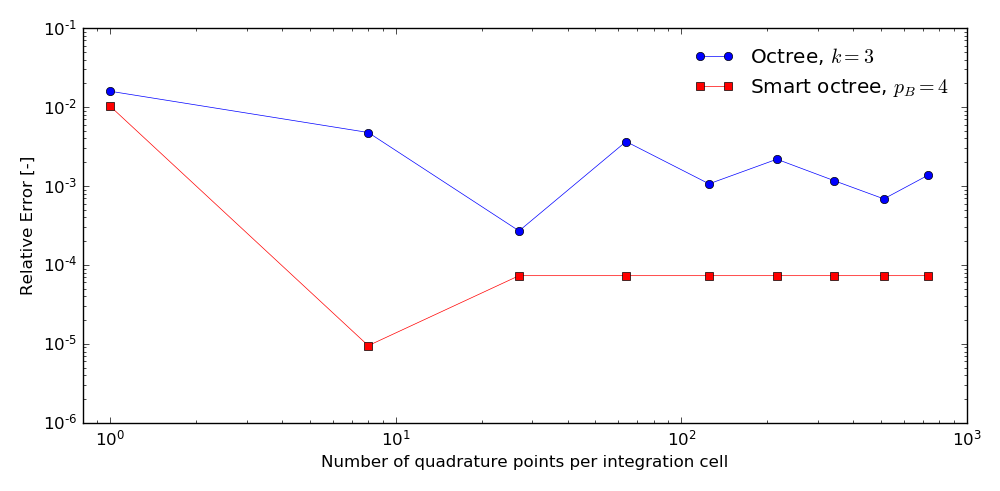
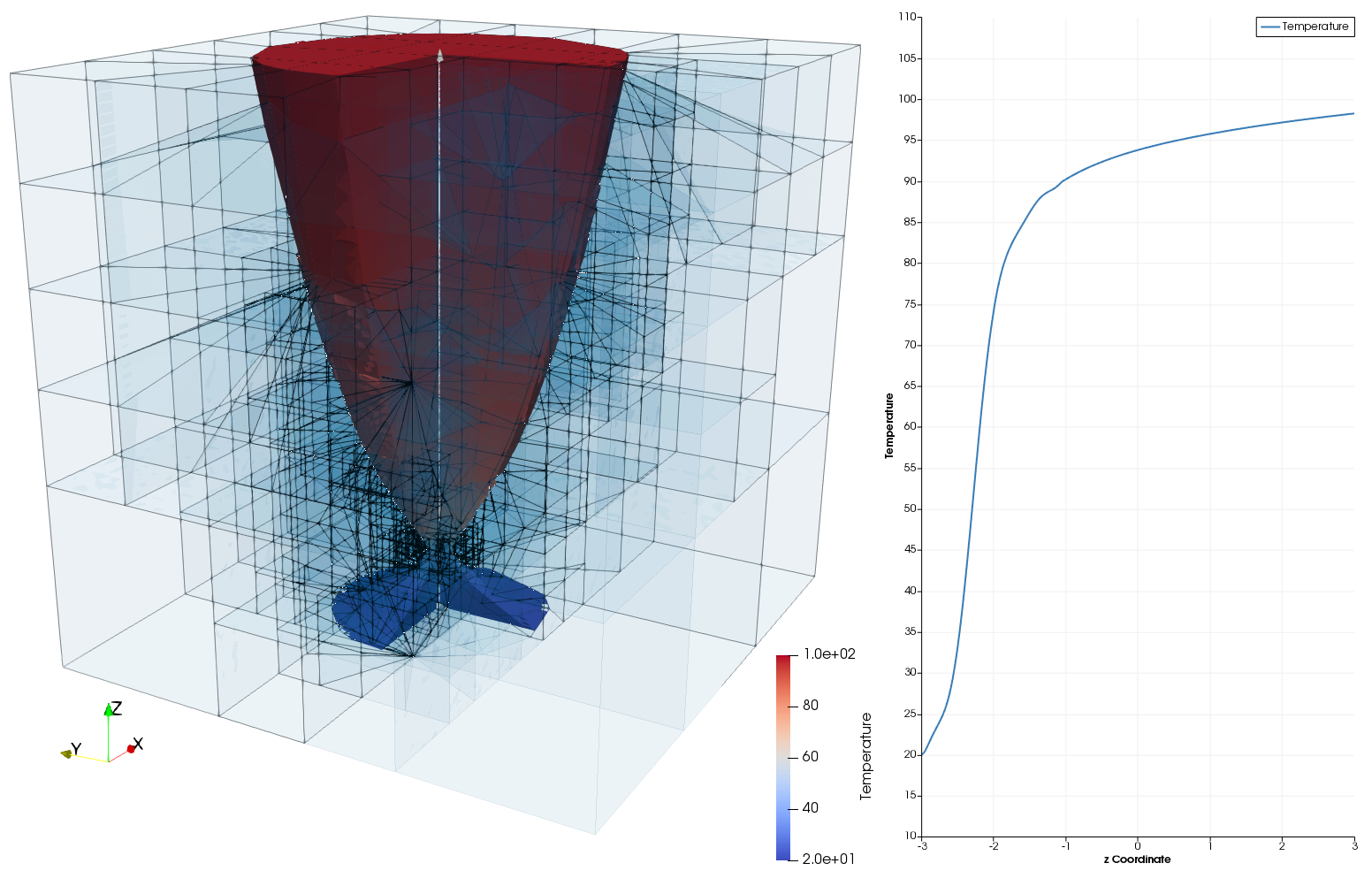
Given that this is not always the case, the aim of this project was the implementation of a version of the method compatible with implicit geometries – such as those originating from Constructive Solid Geometry (CSG). While the general scheme translates smoothly from one representation to the other, it is not trivial to deal with (sharp) feature recognition or to directly recover the non-linear character of the surface. Since the boundary is no longer explicitly stored as part of the representation, recovery techniques to identify vertices and edges become necessary. The present work uses the ideas of Kobbelt et al. from [2]. To verify the resulting setup, a set of benchmark examples representing these difficulties were computed using both the regular- and the smart octree partitioner. Figures 1 and 2 show the integration meshes and relative error in volume respectively for a non-boundary conforming cuboid. In Figures 3 and 4, the process is repeated with a torus. Finally, Figure 5 presensts a full FCM example of a linear thermal problem making use of the new setup.
Fig.1: Octree (left) and Smart Octree (right) partitioning of a non-boundary conforming cuboid
Fig.2: Convergence of the error in volume w.r.t. the number of quadrature points per integration cell. The order of the integration is increased stepwise by distributing, n×n×n quadrature points in every integration cell with n = 1..5
Fig.3: Octree (top), linear Smart Octree (middle), and high order Smart Octree (bottom) partitioning of a torus
Fig.4: Convergence of the error in volume w.r.t. the number of quadrature points per integration cell. The order of the integration is increased stepwise by distributing, n×n×n quadrature points in every integration cell with n = 1..9
Fig.5: Temperature field (left) and centerline (right) of solid wineglass-like structure with Dirichlet boundary conditions on its top and bottom faces
References
| [1] |
László Kudela, Nils Zander, Stefan Kollmannsberger, and Ernst Rank. Smart octrees: Accurately integrating discontinuous functions in 3d. Computer Methods in Applied Mechanics and Engineering, 306:406–426, 2016. |
| [2] |
Leif P Kobbelt, Mario Botsch, Ulrich Schwanecke, and Hans-Peter Seidel. Feature sensitive surface extraction from volume data. In Proceedings of the 28th annual conference on Computer graphics and interactive techniques, pages 57–66. ACM, 2001. |
| [3] |
Martti Mäntylä. An Introduction to Solid Modeling. Principles of computer science principles. Computer Science Press, 1988. |
| [4] |
Jules Bloomenthal and Brian Wyvill, editors. Introduction to Implicit Surfaces. Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 1997. |