Michael Fischer did his honours project at the chair of Structural Analysis under supervision of Prof. Dr.-Ing. K.-U. Bletzinger and in cooperation with the European aerospace company EADS.
Already in the early days of the finite element method in the sixties, it had been discovered that finite elements based upon the virtual work principle may show slow convergence and thus provide inaccurate results. In the seventies the term “locking” established itself for the phenomenon that is characterized by a severe underestimation of the displacements. As a consequence, also the quality of results of structural optimization techniques are heavily reduced, especially in the context of solid finite elements at thin structures. Therefore Michael Fischer investigated already in his diploma thesis geometric locking effects at solid finite elements, presented possible remedies and implemented several improved hexahedral finite element formulations based on the Method of Enhanced Assumed Strains in the research code of EADS.
Most publications on the EAS-method are restricted to hexahedral elements and their 2d-counterparts, the quadrilateral elements. However, there is undoubtedly a huge demand on 3d-elements with triangular base area. This is not only due to the use of automatic meshing methods, but also due to the existence of several geometries in aerospace applications that strongly recommend e.g. pentahedral elements. Therefore, this honours project investigated possibilities to extend the EAS-method to triangle-based solid finite elements as a continuation work of his diploma thesis at EADS.
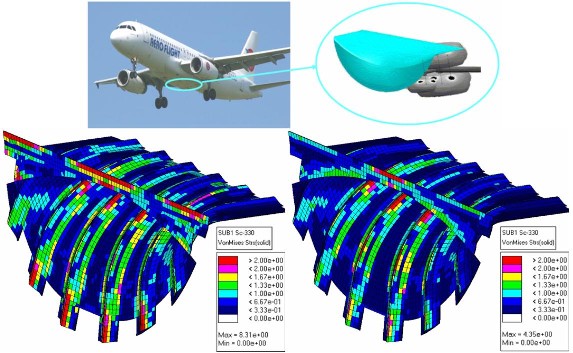 Finite element model of the pressure bulk head of the A320. Left: result of EAS-improved hexahedral and pentahedral finite elements for the Von Mises stresses. Right: solution with “classical” elements based on the principle of virtual work. The strong differences underline the strong need for an improved element formulation.
Finite element model of the pressure bulk head of the A320. Left: result of EAS-improved hexahedral and pentahedral finite elements for the Von Mises stresses. Right: solution with “classical” elements based on the principle of virtual work. The strong differences underline the strong need for an improved element formulation.Starting from the Hu-Washizu principle as variational basis it is shown that the direct application of the EAS-method to triangular-based elements does usually not improve the quality of the results. Therefore an new method to apply enhanced assumed strains has been searched for. Based on the concept of element degeneration, an alternative approach to apply the EAS-method on triangular-based elements is presented. The derivation of the theory, the application for solid elements and an efficient implementation is shown. Several numerical examples illustrate the performance of the enhanced and degenerated elements and confirm the capability of the proposed EAS-concept. Limits of the performance induced by the mesh distortion sensitivity of EAS-elements are examined. Due to the presented approach the EAS method is not restricted to quadrilateral-based elements any more and thus provides an uniform and reliable concept for the elimination of geometric and volumetric locking effects.
