Andreas Apostolatos did his honours project at the Chair of Structural Analysis (TUM), being supervised by Dr.-Ing. Wüchner and M.Sc. (hons) Robert Schmidt .
Numerical quadrature and motivation
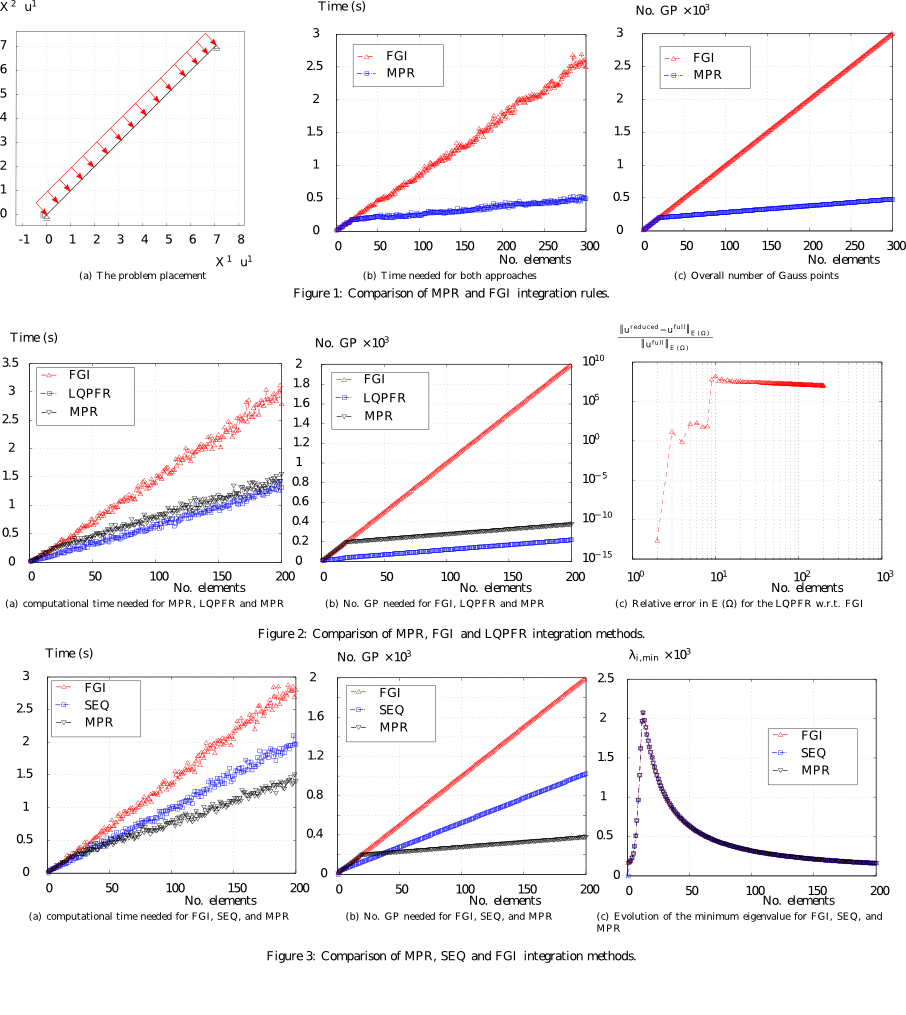
Numerical integration schemes are commonly used for solving integral equations, ordinary or partial differential equations, the computation of every free-form surface area and to other various applications. In particular, for the numerical treatment of partial differential equations using the Finite Element Method (FEM), the most computational effort can be attributed to the numerical approximation of the underlying integrals. From the above, it is clear that the investigation of efficient algorithms for the numerical integration is one of the main tasks of numerical analysis. The general Newton-Cotes quadrature is compared to the Gaussian quadrature for a simple function, see the Figure below.
Integration efficiency for the isogeometric Euler-Bernoulli beam
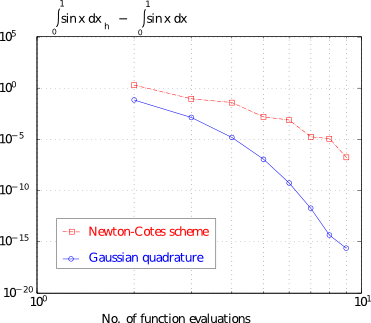
Isogeometric Analysis, abbreviated by IGA, eased the development of numerical schemes for problems which attain variational index higher than 1 due to the high inter-element continuity that one can use. It is well known that the Euler-Bernoulli beam belongs to this kind of problems attaining variational index equal to 2. The integrand of the membrane part is of polynomial degree 2(p-1) and the integrand of the bending part is of polynomial degree 2(p-2). There are two ways to compute numerically the underlying integrals. The one is to perform a uniform Gaussian quadrature for both parts, taking into consideration only the part with the highest polynomial degree i.e. 2(p-1). The other one is to take advantage of the fact that the membrane and the bending part of the stiffness matrix attain different polynomial orders, and integrate those differently, selecting the minimum amount of Gauss points such that to obtain an appropriate integration. It has been shown that uniform integration is more efficient than the selective one with respect to the time, see figure below.
Efficient quadrature rules in isogeometric analysis
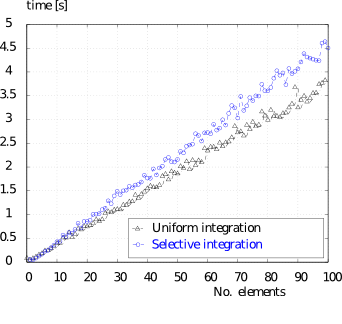
We have considered the Mid-Point Rule, abbreviated as MPR, by using only one integration point at the middle of each interior knot span but full quadrature at the p+1 first and last knot spans. That is because at the p+1 first and last knot spans there exist basis functions which have support into less than p+1 knot spans and for which the MPR would introduce zero energy modes. The Full Gauss Integration, abbreviated as FGI, is compared to the MPR in terms of the number of Gauss points and the time, for a simple straight Euler-Bernoulli beam element subject to uniform pressure load. Integration in both cases is exact thus both solutions are the same. The results can be found in the set of Figures 1. Another method that has been investigated is the modified MPR where at the p+1 first and last knot spans we use as many Gauss points as needed to ensure full rank of the stiffness matrix and we abbreviate this as LQPFR (Least Quadrature Points for Fully Ranked Stiffness Matrix). From the set of Figures 2 it is evident that ensuring fully ranked stiffness matrix is not sufficient for obtaining reasonable in terms of accuracy results. Additionally the efficiency gain is negligible. As last the Simple Efficient Quadrature rule is tested. This is abbreviated as SEQ. New locations for the quadrature points are computed using the FGI, the new locations being optimal with respect to the given knot span and polynomial degree of the NURBS curve (eq. surface). The results suggest that the method is highly reliable providing also significant speed-up of the numerical integration, see set of Figures 3.