Mohamed Khalil did his honours’ project at the Chair of Structural Analysis (LS Statik, TUM) and International Center for Numerical Methods in Engineering (CIMNE). The work was supervised by MSc. Vicente Mataix (CIMNE), Dr.-Ing. Riccardo Rossi (CIMNE), and Dr.-Ing. Roland Wüchner (TUM).
Introduction
Contact mechanics is an abundant phenomena in our daily lives and engineering applications. With the increasing capabilities in the field of computational mechanics, the applications in which contact mechanics is involved such as sheeting metal forming processes or tribology become attractive to investigate in depth. Hence, research has been directed towards improving the robustness of the adopted formulations and boost their numerical performance.
The Physics of Contact
A contact mechanics problem is a multi-body solid mechanics problem, with an additional set of mixed-type boundary conditions described at the boundary interface, γc. The condition, in its general form, is defined by the Karush-Kuhn-Tucker (KKT) condition as,
The Mathematical Representation of Contact
Since the contact mechanics is a solid mechanics problem described by a potential function, W(u), and constrained by the set of contact boundary conditions, G(u), incorporated in the KKT, the problem in hand can be written, from a mathematical perspective as,
Important to note is that the contact mechanics problem is a classified as a constrained minimization problem, where the objective function to be minimized is the potential of the system, and the set of constraints are the KKT condition constraints applied to the active contact interface. For this class of problems, various approaches are present to enforce the said constraint, such as the penalty method or the Lagrange multiplier method.
Employing the Lagrange multiplier method, the mathematical representation of the contact problem is written as
The Finite Element Discretization
Since the contact interface needs to be discretized in space using FE, the definition of the contact constraint needs to be consistently discretized. The segment-to-segment approach is one way of discretizing interface problems in general. Here, the contact constraint is satisfied in an integral sense over the complete interface, in a discrete description over all finite elements e, as follows
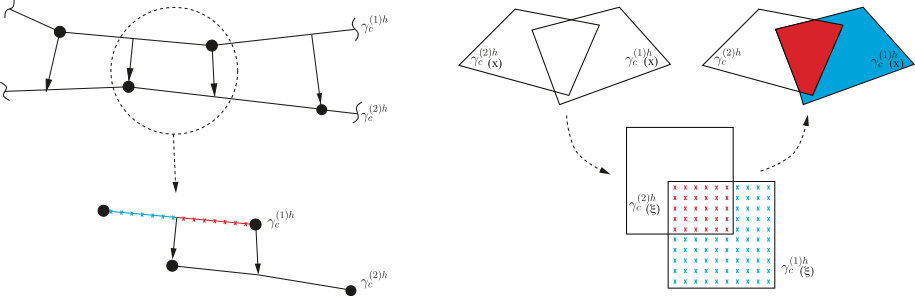
The integral is evaluated on one side of interface, called the slave surface. To evaluate the integral accurately, it must be evaluated on the active portions of every element. Since it is common to have non-matching interface meshes, or having such mismatchness due to relative sliding, the integral can’t be evaluated simply over the entire element’s domain, but only over a certain sub-domain. This results in a discontinuous integral, which can’t be treated by Gauss numerical integration. Instead, a collocation scheme is applied; where integration points are uniformly distributed over the domain of the element, and the integral is evaluated at points whose projection lies inside the element on the opposite surface, as shown in Fig. 31.
 |
|
Fig. 1: The collocation integration scheme in 2D and 3D. The red and blue sub-domains are the active and inactive, respectively, sub-domains of the slave element.
|
Robustness Assessment
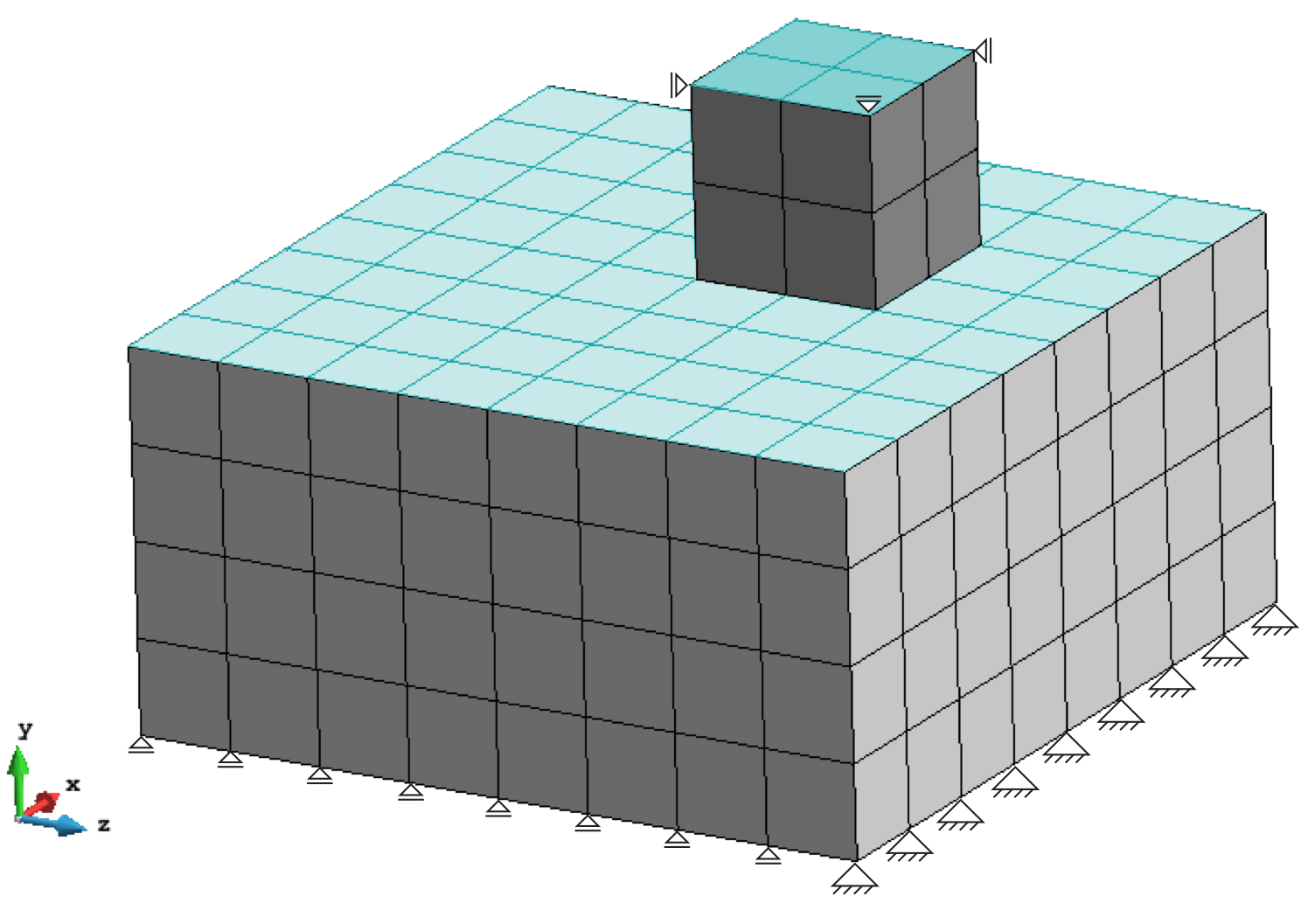
In previous work by the author, the proposed method has shown good results in 2D. An extended formulation in 3D is tested for roubstness using the classic patch test. In this test, as shown in Fig. 2, two blocks are initially in contact, and a constant pressure, P, is applied to the non-contacting top surfaces (colored in light blue). A consistent formulation should transfer a vertical stress component, σyy, along the interface which is equal to the applied pressure.
 |
 |
|
Fig. 2: Mesh and boundary conditions of a patch test in 3D.
|
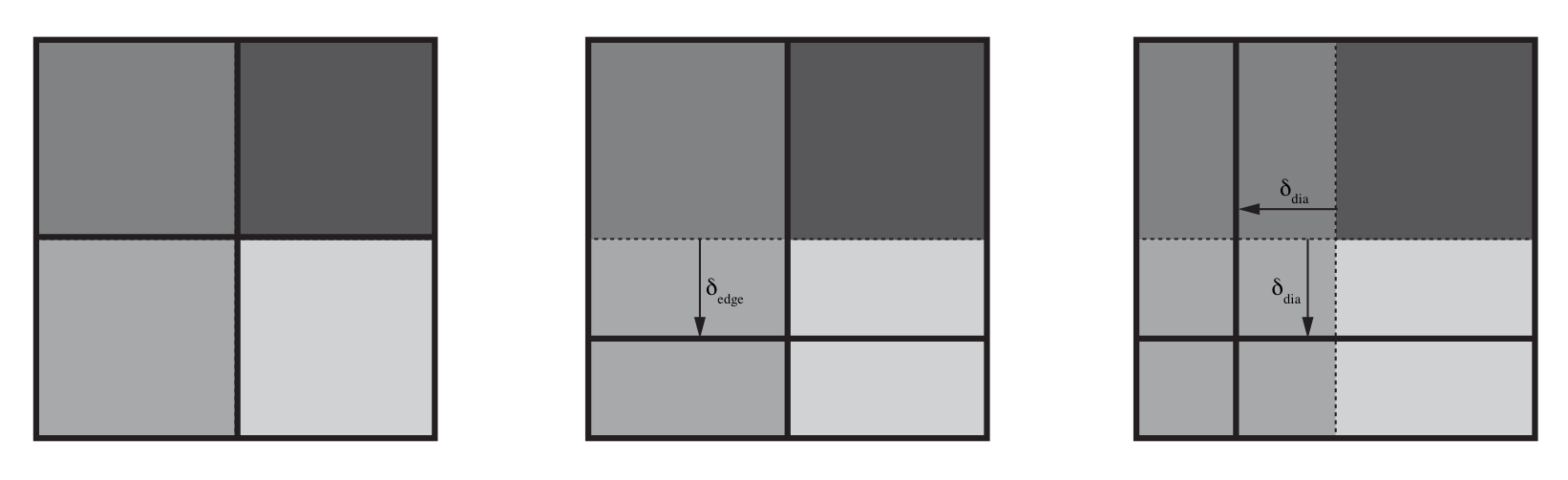
Fig. 3: Different mistmatchness types and measure of mismatchness; from right, no, edge (δedge) and diagonal mismatchness (δdia).
|
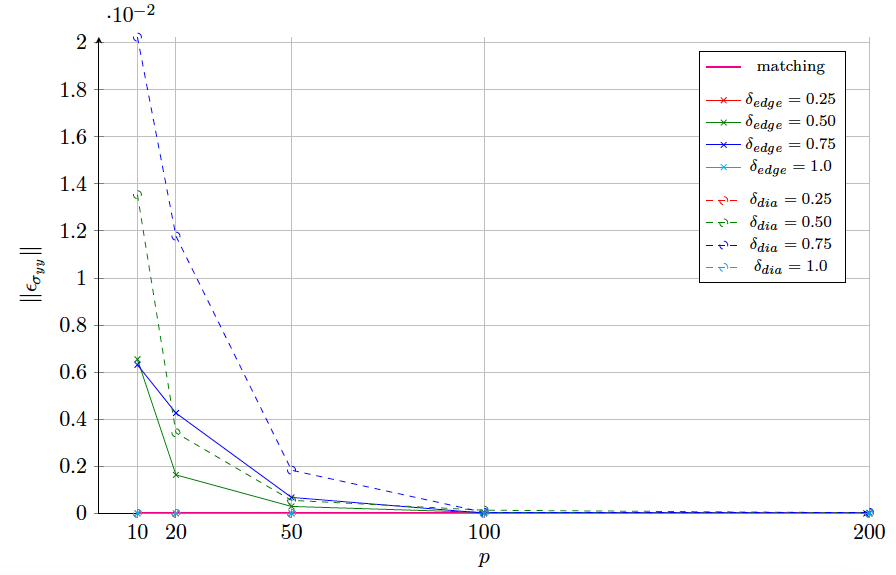
The error L2-norm in the simulation results, ||εσyy||, is calculated as ||εσyy|| = || ( σyy, i / P ) – 1 ||. Both matching and non-matching interface meshes, see Fig. 3, are used to evaluate the error. Fig. 4 shows the evolution of the error as the number of the number of integration points changes for every case. It is clear that a very high number of integration points is required for non-matching interface meshes, which gives an indication about the relatively high cost of the proposed approach in 3D, especially for such a basic example. As a conclusion, a more accurate integration method is recommended for 3D, such as mortar segmentation presented in [1].
 |
|
Fig. 4: Evolution of error with respect to the number of integration points used for different levels and cases of mesh mismatchness.
|
;
