Room Acoustics Simulation

Yunyun Ni, Evelyn Otero

Room Acoustics Simulation was a team project of two students of the CE-branch of the BGCE.

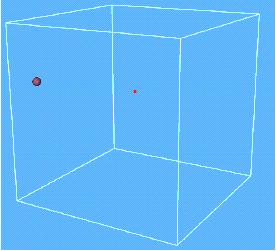
Left: Geometry of the room, sound sender and listener, Right: 8281 rays represented

For a long time in order to know the propagation of the sound in a specific room we had to go through several experiments, measurements in different points of the room which require equipments, time and money. Then, through this project our goal is to provide a solution based on simulations in order to analyse, predict the sound in given points of a room depending on the wall characteristics.

The work consists in exploring two approaches for room acoustics simulation, one derived from computer graphics, the raytracing method, allowing for a fast characterization of sound propagation from multiple sources to a certain receiver, the other solving the wave equation for the whole domain.

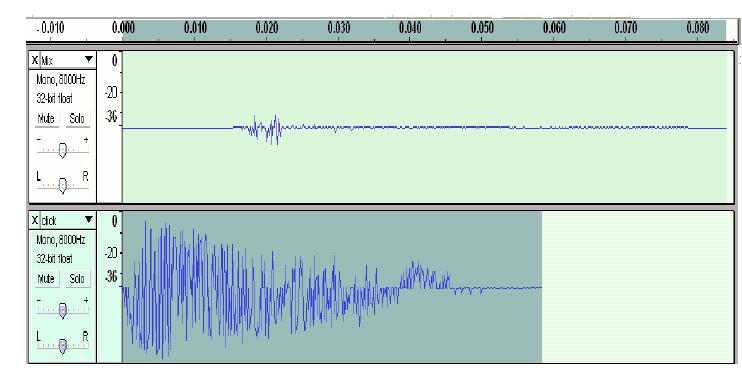Top: The auralisation result at the listener, Bottom: Sound source

For the room acoustic simulation using ray tracing method the following steps were taken: Firstly set up the geometry model of the room and listener, and accordingly apply the geometry ray tracing algorithm: ray-sphere intersection,ray-plane intersection etc. In the algorithm, also consider the environment condition of the room, people’s volume, wall absorption and air absorption etc. Base on the results of the geometry ray tracing, a digital filter library was used for the auralisation approach. And also a sound editor software for the mixture of the sound.

Concerning the second method, the following points have been treated:

– Analyse of the discretization schemes: Finite Difference

– Treatment of the Boundary Conditions (BC): Homogeneous Dirichlet BC, Homogeneous Neumann BC

– Evolution from a one dimensional problem to a third one Visualization (Paraview) and Audio files generation

The results have been satisfactory and as expected, however the simulation through the wave equation computation shows a strong sensitivity regarding the implementation of the boundary conditions in a time dependent problem. In fact you can easily end up with ones which add energy to the system and don’t behave as the real wall parameters.

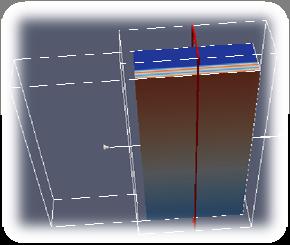Left: 2D-Homogeneous Dirichlet, Middle: 2D Homogenous Neumann, Right: 3D-Homogeneous Dirichlet