Theresa Pasch did her Honour’s project at the Associate Professorship of Computational Mechanics (TUM) and
was supervised by Lukas Leidinger and Prof. Dr.-Ing. habil. Fabian Duddeck.
In contrast to classical FEM, where the computation is done on a Finite Element model, Isogeometric Analysis (IGA) enables the computation directly on a CAD geometry. To deal with trimmed multi-patch CAD geometries, IGA was extended to Isogeometric B-Rep Analysis (IBRA) where trimmed patches are coupled by penalty based B-Rep elements [3]. The advantage of the integration of engineering design and analysis process was the motivation to use IBRA for vehicle crash simulations. Crashworthiness of a vehicle is a highly non-linear and dynamic problem which is solved by explicit time integration methods. Therefore IBRA was recently extended to Explicit IBRA where a special treatment of the time steps has to be considered [1]. Explicit time integration is computationally faster and more robust for crash simulations than implicit methods but it is only conditionally stable. That means, that the maximum time step is bounded by a critical time step which depends on the maximum system eigenfrequency.
By coupling patches with penalty based B-Rep elements, additional stiffness but no additional mass is introduced to the system, which leads to an increase of the maximum system eigenfrequency. This results in a decrease of the stable time step and a rise of the computational costs. High penalty factors are desired for an accurate solution but they also introduce more stiffness to the system, which results in an even smaller time step. To overcome this goal conflict, selective mass scaling was implemented and validated within the scope of this Honours Project [4]. Mass scaling is based on the idea that the influence of the additional stiffness on the system eigenfrequency can be compensated by adding as well mass at the affected control points. The goal is to eliminate the time step reducing effect of penalty coupling by selective mass scaling and to achieve the time step size without penalty coupling (goal time step). An overview of the problem description is given in Figure 1.
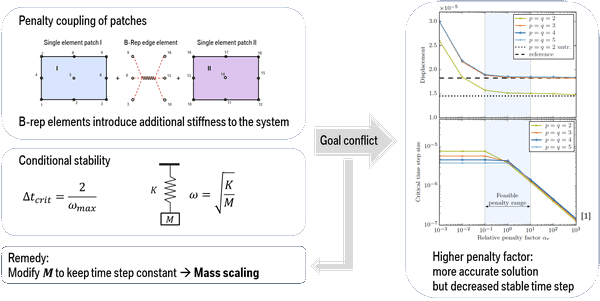 |
In Explicit IBRA the mass is assigned to control points, i.e. lumped masses are used. For each control point an individual mass scaling factor is computed, which is the ratio of the mass that is needed to achieve the goal time step and the initial control point mass. A nodal eigenvalue respectively nodal time step is essential, which can be approximated using Gershgorin circle theorem [2]. The simulation of different benchmark examples with and without selective mass scaling shows that mass scaling serves as a remedy to avoid the decrease of the critical time step due to penalty based B-Rep coupling. The added mass to achieve this might influence the system response, especially when inertia effects play a role. Exemplarily the mass scaling results for a Pinched Cylinder taken from [1] are shown in Figure 2.
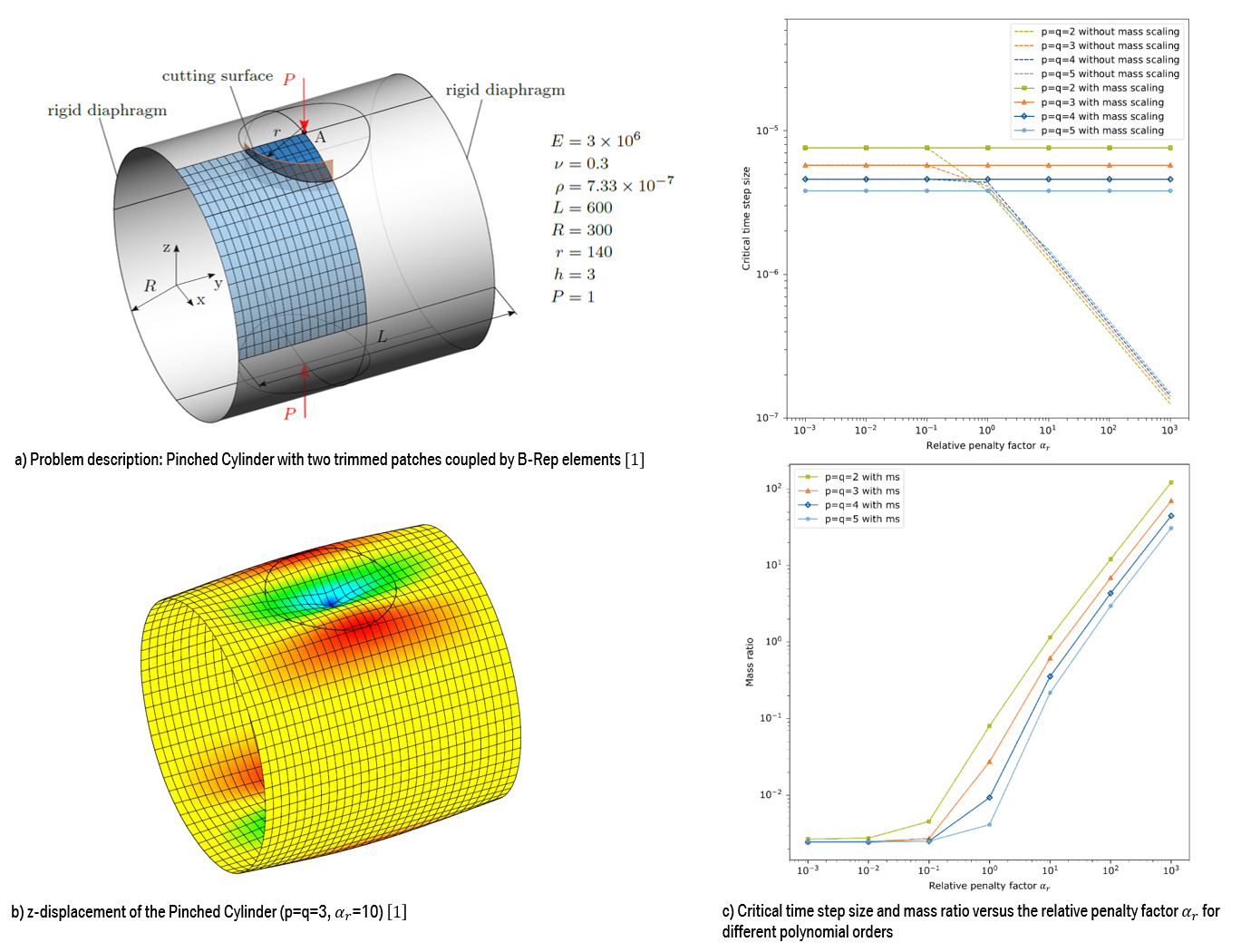 |
