Supervision: Tobias Preclik in Cooperation with Thorsten Pöschel, Institute for Multiscale Simulation.
Problem Formulation
The aim of this project is to model and simulate an actual physical experiment as accurately as possible in order to improve and support the understanding of the effects that can be observed. The experiment consists of a hollow cylinder with a diameter of approximately 30cm and a depth of around 5cm. The bottom half of this cylinder is filled with a silicium carbid granulate that has a grain size of about 0,5mm. This cylinder gets rotated with a constant angular velocity that is chosen such that a permanent particle flow on the surface can be observed. At the same time the particles underneath the surface do not show any movement besides the applied rotation to the cylinder. The interesting observation is that in the beginning one only sees the constant particle flow on the surface. But at apparently random moments a collapse occures: A state of unstable equilibrium breaks and the surface in the higher regions of the incline drops several percent. In consequence, the density of the volume decreases. One application of this experiment is that silos, filled with granular material, seem to break for no reason and the observed collapses in the experiment might help establish a theory explaining such events. In order to gain a better comprehension of this process, i.e. when and why the granulate collapses, the project team is setting up a simulation based on the physics engine pe of the Chair for System Simulation. Such a simulation offers the possibility to collect data that cannot be recovered from the physical experiment, e.g. the forces between the particles or the number of contacts of single particles right before a collapse. Thus, the aim is to get an insight on the reasons for the instabilities of these granular materials by recovering the collapses within the simulation as well as offering tools to store and analyse the relevant data.
Functionality
Particle Generation
The project offers a set of different particle types to be used, with different properties and behaviour. All designs are composites of the basic pe physics engine rigid body shapes. The createParticle() method uses the pe-provided methods to create the basic shapes, randomizes them and binds them in a Union. This randomizing affects both the size of the single basic shapes as well as their position and angles to each other in a reasonable range. Size scales and material properties can be specified to further parametrize the particles. Different particle shapes under investigation can be found in Figure 1.
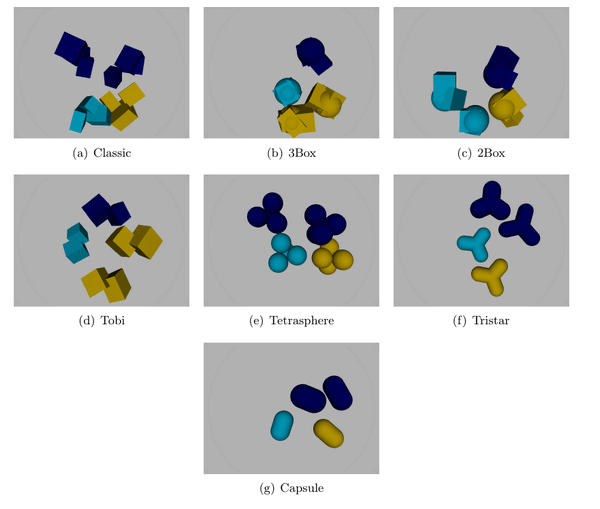
Figure 1.
Parallelization
The pe physics engine enables code to be run on multiple processors with the help of MPI for interprocess communication. To be able to use MPI, the simulation domain has to be divided into subdomains, where every process is responsible for particles within one subdomain. To achieve good performance, there are a couple of points one has to keep in mind when designing a domain decomposition: The number of particles in each subdomain should be approximately equal, because this number determines the compu- tational effort for the process handling this subdomain. As the processes communicate in each timestep, the slowest process determines the overall speed of the simulation, thus load balancing is very important. Secondly, the communication overhead should be as small as possible. This overhead is determined by both the number of neighboring processes (a lot of neighbors will lead to a lot of send and receive operations) and the size of the border of the subdomain (large boundaries could mean a large amount of particles moving to another subdomain or being in contact with them, which in turn means a lot of data to be sent). The used decomposition method can be specified in the parameter file. The project provides three different domain decompositions, which are called the stripes-, pizza- and spiderweb-decomposition. The three of them are depicted in Figure 2.

Figure 2.
All three decompositions have two properties in common: First of all, only the bottom half of the cylinder is divided according to the scheme, the top half is always managed by only one process. This is assuming that only approximately one half of the cylinder is filled with particles, thus a decomposition of the whole cylinder would result in a lot of processes without any particles, wasting computational resources. When the cylinder is rotating, a plane will finally develop on which particles will slide from top to bottom. To compensate for the non-horizontal orientation of this plane, all decompositions can be rotated to ensure that all processes are fully loaded except that one on the top. The degree of this rotation can be specified in the parameter file. Figure 3 shows the typical particle pathlines of a simulation setup.
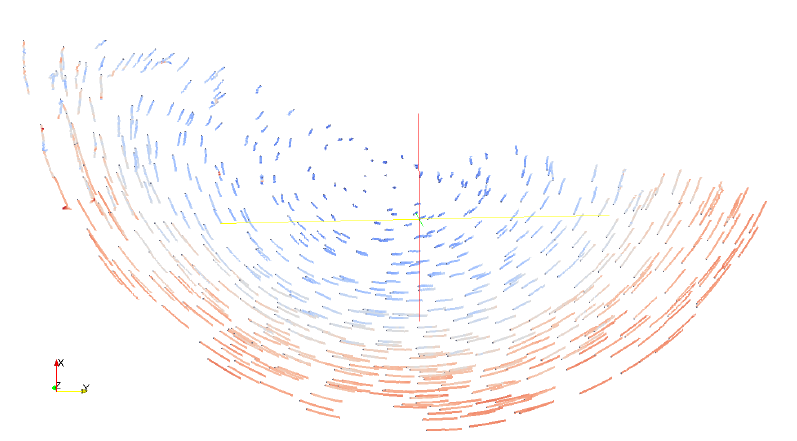
Figure 3.
The full final report is available here.
