Supervision: Dr. Björn Gmeiner, Prof. Dr. Ulrich Rüde (Chair for System Simulation, Computer Science, Friedrich-Alexander-Universität Erlangen-Nürnberg)
Task Description
The Terra-Neo project, part of the German Priority Programme 1648 to develop software for exa-scale computing, deals with the numerical simulation of Earth mantle dynamics which poses a grand challenge in scientific computing acquiring a fine enough spatial and temporal resolution. To solve the underlying Stokes equations the Galerkin Finite Element Method (FEM) together with a multigrid algorithm is used to achieve the necessary performance. Due to the high Péclet-number occurring in Earth mantle dynamics, the energy equation can be approximated by a pure advection equation for the temperature. However, to be able to solve this equation with FEM artificial diffusion has to be added in order to stabilise the procedure. Unfortunately, this approach disturbs and consequently falsifies the obtained solution significantly. Instead of the physically expected thin flow channels, which transport material from the core to the surface of the Earth, one obtains broad channels as a result of the increased diffusion. Therefore, the task of the BGCE Honours Project is to develop and evaluate unconventional discretisations of the temperature equation that tackle the problem of artificial diffusion.

Figure 1: Earth mantle simulation of the Terra-Neo project and schematic representation of the underlying grid (shadowed).
Bresenham Method
The first method is based on the Bresenham algorithm, which originates from the field of computer graphics and is used there to draw straight lines in a discretised domain. This algorithm is especially designed to maintain sharp edges and thus can be physically interpreted as a diffusion-free transport of a quantity. The developed method is built upon these key ideas and uses offset values to determine the advection direction of the temperature.
Lagrangian Method
In contrast to the grid-based Bresenham Method, the second algorithm – denoted as Lagrangian Method – makes use of particles for the temperature transport. These particles do not interact with each other and move through the domain according to the underlying velocity field by carrying the relevant quantities. Since temperature and velocity are nevertheless given on an underlying grid, interpolations between particles and grid vertices are necessary to link Lagrangian and Eulerian specification.
Results
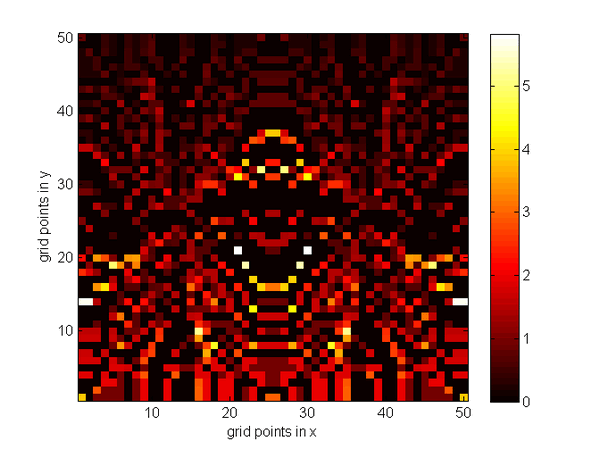
Simulations in one- and two-dimensional domains reveal inherent shortcomings of the Bresenham Method stemming from the fact that the values of vertices will occasional merge causing unphysically high temperature values in certain regions and at the same time empty vertices in other regions. This problem cannot successfully be overcome by different attempts like partial jumps and redistribution kernels. On the other hand, the Lagrangian Method yields promising results but special care has to be taken in order to avoid the appearance of empty vertices seen as black spots in the picture. A combination of random initial particle placement, increasing the number of particles and using filling kernels is found to effectively counteract this problem.
 |
 |
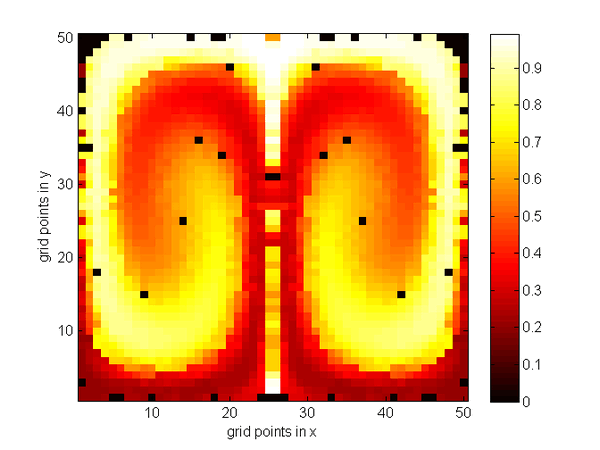 |
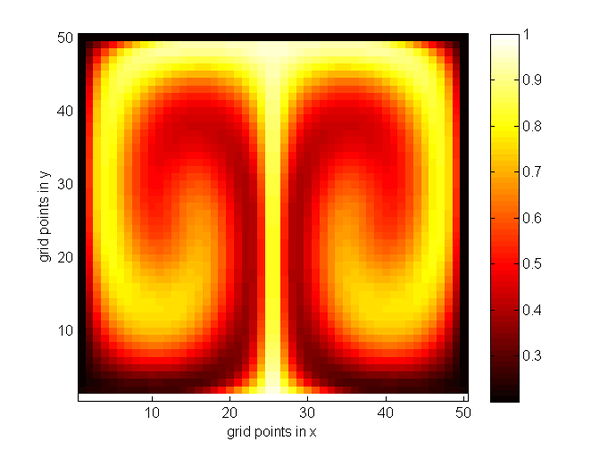
Figure 2: Outcome of the three different algorithms (Upwind scheme, Bresenham Method, Lagrangian Method) on a 50×50 grid. The initial temperature profile decreased linearly in y-direction, the velocity field is the analytical solution of the Stokes equations with two convection chambers.
Conclusion
Due to the unsolvable problems in the Bresenham Method, we drop this approach and suggest to use the Lagrangian Method. We further extend this method to work on triangle and tetrahedron grids to offer an interface to the implementation of the Earth mantle dynamics solver of the Terra-Neo project. Additional advantages of the proposed method are the parallelisation capability, a straight-forward extension for advecting other physical quantities and the possible inclusion of physical diffusion in an operator-splitting approach.
 |
 |
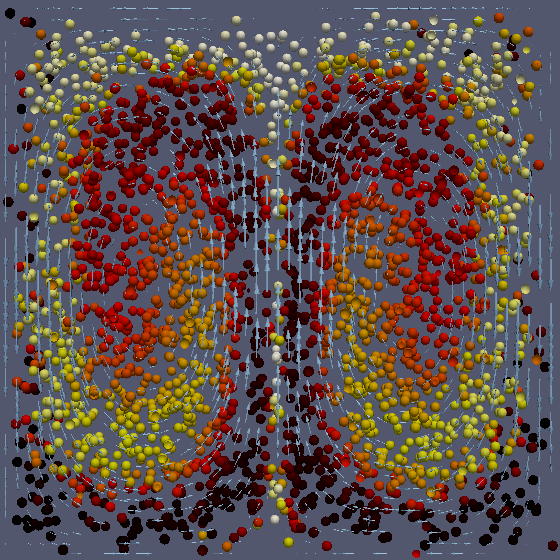 |
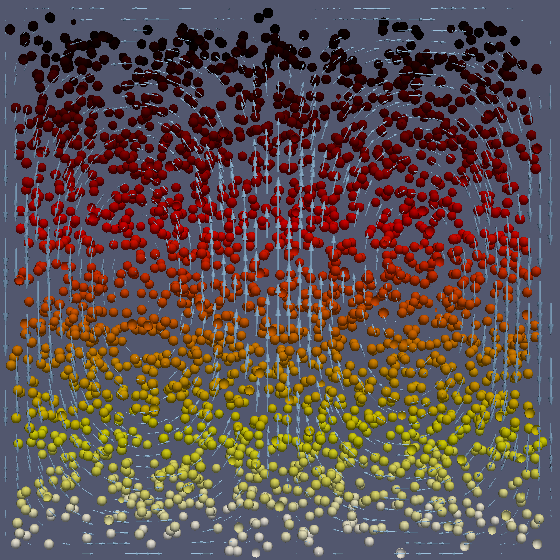
Figure 3: Evolution of a subset of the particles which are coloured by its temperature. The velocity field is visualised with light blue arrows.
For more information see the full final report here.
