Finite Cell Method (FCM) is an embedded domain method using high order polynomial shape functions [1]. The basis idea is depicted in Figure 1, a complex shape domain Ω is embedded within a much simpler fictitious domain Ωfict. On Ωfict a cartesian grid can be easily generated, each cell of the grid defines a local support for a set of high-order polynomial shape functions, i.e. it defines an element, which in this context is called cell in order to distinguish it from the classical FEM-element. The original shapes is recoverd introducing a discrete parameter α into the bilinear operator of the weak form. The value of the parameter α is set to 1 if inside Ω and to a “close to” 0 value(in general value of α are chosen within the interval [10-10, 10-14] in order to avoid ill-conditioning of the linear system) if outside, finally the integration is performed via space-tree using gaussian quadrature rule.
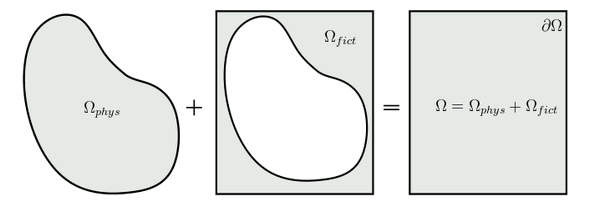
Figure 1: The Finite Cell Method embedding process
Motivation
One of the main issues of the FCM is the application of the Dirichlet boundary conditions, in fact these boundary conditions cannot be directly enforced at the nodes as in classical FEM but they can be enforced only in a weak sense, i.e. introducing these conditions into the weak form of the problem. Many different methods allow us to weakly apply boundary conditions (e.g. penalty method, Nitsche’s method,…), in this project we want to investigate the results obtained using the Lagrange Multipliers Method together with the FCM in the context of contact mechanics [3].
Lagrange Multipliers Method in FCM
As mention before the FCM avoid mesh generation, but in order to apply the Lagrange Multipliers Method we need to generate a local support for the Lagrange multipliers shape functions. The so-called lagrangian (or boundary) element is thus created making use of the fictious domain, over this domain a new cartesian grid (which does not necessarily correspond to the FCM-grid) is generated, then performing marching square algorithm and line-search projection we obtain the boundary elements at each cell of the grid.
The dual problem obtained using Lagrange multipliers cannot be easily solved neither by direct nor iterative solver, this turns out being a crucial issue in particular for non-linear problems. Therefore we need a more robust and easy-to-solve method if we want to deal with contact mechanics problems. In order to overcome such a problem we have then implemented a modified version of the Lagrange multipliers method, the so called augmented Lagrange multipliers method. In this method an additional penalty term is introduced in order to make the system easier to solve, thus a classical direct solver can be employed to solve the dual problem using a Newton-Raphson iteration scheme.
Results
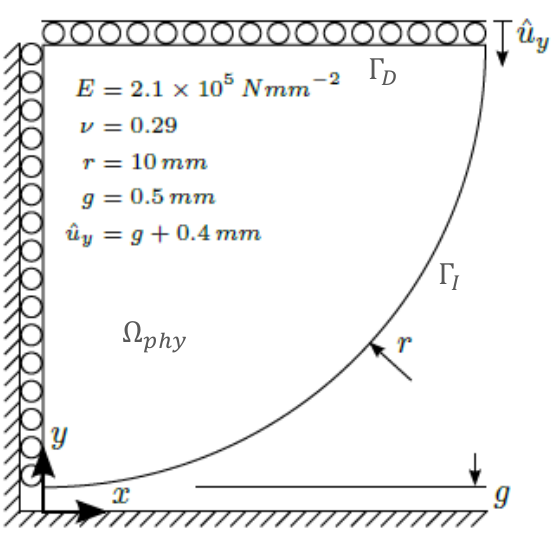
In order to validate the method we have chosen a classical 2D Hertz problem as depicted in Figure 2, the symmetry condition on the left edge and the prescribed displacement on the upper edge are enforced strongly on the cells, while the contact condition at the interface ΓI is enforced via augmented Lagrange multipliers.
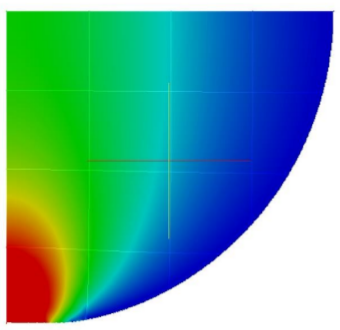
Figure 3 shows the Von Mises stress distribution using a 4×4 FCM cartesian grid, an 8×8 grid for the lagrangian elements generation and polynomial order p=5 for the physical ansatz space. The smooth stress distribution results from the high-order shape functions used to approximate the solutions, which allow us to capture the stress behaviour with an higher continuty.
First we have investigated the behaviour of the method using different ansatz spaces for the Lagrange multipliers and for the field variables. In Figure 4a we observe the contact pressure distribution using first Legendre polynomials for both the physical and the lagrangian ansatz space and then using Legendre polynomials for the physical ansatz and B-Splines as shape functions for the boundary elements. The two results are almost identical, therefore we can consider our method independent from the chosen ansatz of the Lagrange multipliers.
In a second step the influence of different parameters has been analysed. In Figure 4b are presented the effects of the lagrangian element polynomial order on the normal pressure at the contact interface, in particular we observe that increasing the lagrangian ansatz order we have at the beginning a strong improvement in the results and later this effect levels off. Furthermore performing a study on the convergence rate for the Newton-Raphson solver we observe that increasing the lagrangian ansatz order the convergence rate will decrease. The same behaviour can be observerd with respect to the number of Gauss points used to integrate the boundary element. For both these parameters we can conclude that there is an optimal value which depends on both the physical problem and the chosen ansatz order of the solution ansatz space.
Finally in Figure 4c is presented the effect of adaptivity on the contact pressure distribution. Here a simple h-refinement was performed towards the contact interface discontinuity, in particular we observe that making use of a refinement scheme allow use to strongly reduce the pressure undershoot at the discontinuity. In this project adaptivity has not been implemented for the lagrangian elements, therefore the grid used to generate the boundary elements does not change, extend adaptivity also to the lagrangian mesh might be a promising and interesting outlook for further researches.
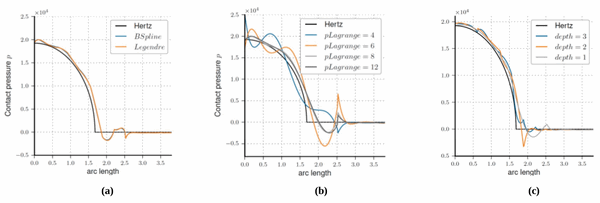
Figure 4: Normal pressure at the contact interface
Bibliography
[1] J. Parvizian, A. Düster and E. Rank, Finite cell method – h- and p-extension for embedded domain problmes in solid mechanics. Computational Mechanics, 41:121-133,2007.
[2] T. Bog et al., Normal contact with high order finite elements and a fictitious contact material. Computers & Mathematics with Applications 05/2015; 70(7).
[3] P. Wriggers, Computational Contact Mechanics. Springer-Verlag, 2007.
